题目内容
定义域(-1,1)上的函数f(x)满足:f(x)-f(y)=f(
),当x∈(0,1)时,有f(x)<0,若P=f(-
)+f(-
),Q=f(-
),R=f(0),则P,Q,R的大小关系是( )
| x-y |
| 1-xy |
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 2 |
| A、R>Q>P |
| B、Q>P>R |
| C、P>R>Q |
| D、R>P>Q |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:根据条件判断函数的奇偶性和单调性,利用函数的奇偶性和单调性结合抽象函数的性质即可得到结论.
解答:
解:令x=y=0,得f(0)=0.
又当x=0时,f(0)-f(y)=f(-y),即f(-y)=-f(y).
∴对任意x∈(-1,1)时,都有f(-x)=-f(x).
∴f(x)为奇函数.
则P=f(-
)+f(-
)=f(-
)-f(
)=f(
)=f(-
),
(2)任取x1,x2∈(-1,1)且设x1<x2
f(x1)-f(x2)=f(
),
∵-1<x1<x2<1,∴x1-x2<0,则|x1x2|<1,
∴1-x1x2>0,
∴
<0,
∵当x∈(0,1)时,有f(x)<0,
∴f(x1)-f(x2)=f(
)<0,
即f(x1)<f(x2),
则函数f(x)在(-1,1)上为增函数,
∵-
<-
<0,
∴f(-
)<f(-
)<f(0),
即R>P>Q,
故选:D
又当x=0时,f(0)-f(y)=f(-y),即f(-y)=-f(y).
∴对任意x∈(-1,1)时,都有f(-x)=-f(x).
∴f(x)为奇函数.
则P=f(-
| 1 |
| 5 |
| 1 |
| 11 |
| 1 |
| 5 |
| 1 |
| 11 |
-
| ||||
1+
|
| 2 |
| 7 |
(2)任取x1,x2∈(-1,1)且设x1<x2
f(x1)-f(x2)=f(
| x1-x2 |
| 1-x1x2 |
∵-1<x1<x2<1,∴x1-x2<0,则|x1x2|<1,
∴1-x1x2>0,
∴
| x1-x2 |
| 1-x1x2 |
∵当x∈(0,1)时,有f(x)<0,
∴f(x1)-f(x2)=f(
| x1-x2 |
| 1-x1x2 |
即f(x1)<f(x2),
则函数f(x)在(-1,1)上为增函数,
∵-
| 1 |
| 2 |
| 2 |
| 7 |
∴f(-
| 1 |
| 2 |
| 2 |
| 7 |
即R>P>Q,
故选:D
点评:本题主要考查抽象函数的应用,利用函数奇偶性和单调性的定义判断函数的单调性和奇偶性是解决本题的关键.综合性较强,有一点的难度.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
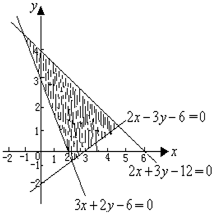
表示如图中阴影部分所示平面区域的不等式组是( )

A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
自然数1,2,3,…,n按照一定的顺序排成一个数列:a1,a2,…,an.若满足|a1-1|+|a2-2|+…+|an-n|≤4,则称数列a1,a2,…,an为一个“优数列”.当n=6时,这样的“优数列”共有( )
| A、24个 | B、23个 |
| C、18个 | D、16个 |
规定:若函数f(x)的图象经过某种变换后所得图象对应函数的值域与f(x)的值域相同,则称这种变换是f(x)的T变换,下面给出四个函数及其对应的变换,其中不属于f(x)的T变换的是( )
| A、f(x)=(x-2)2:将函数f(x)的图象关于直线x=3对称 | ||||
| B、f(x)=2x-3-4:将函数f(x)的图象关于x轴对称 | ||||
| C、f(x)=2x-4:将函数f(x)的图象关于直线y=x对称 | ||||
D、f(x)=sin(2+
|
下列四个命题:
①时间、速度、加速度都是向量;
②零向量的长度为零,方向是任意的;
③若
,
是单位向量,则
=
;
④若非零向量
与
是共线向量,则A、B、C、D四点共线,其中正确命题的个数为( )
①时间、速度、加速度都是向量;
②零向量的长度为零,方向是任意的;
③若
| a |
| b |
| a |
| b |
④若非零向量
| AB |
| CD |
| A、0 | B、1 | C、2 | D、3 |
自点A(-1,3)做圆(x-2)2+(y+1)2=9的切线,则切线长为( )
| A、3 | B、4 | C、5 | D、6 |