题目内容
已知数列{an}的前n项和为Sn,且Sn=2-(
+1)an(n∈N+).
求证:数列{
}是等比数列;
设数列{2nan}的前n项和为Tn,求数列{
}的前n项和为An.
| 2 |
| n |
求证:数列{
| an |
| n |
设数列{2nan}的前n项和为Tn,求数列{
| 1 |
| Tn |
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:首先由数列递推式求得数列的首项,取n=n-1后作差即可证得数列{
}是等比数列;由等比数列的通项公式求出数列{an}的通项公式,代入{2nan}后由等差数列的前n项和求得Tn,取倒数后由裂项相消法求得数列
{
}的前n项和为An.
| an |
| n |
{
| 1 |
| Tn |
解答:
证明:由Sn=2-(
+1)an,①
取n=1,得a1=S1=2-(2+1)a1,即a1=
;
当n≥2时,Sn-1=2-(
+1)an-1,②
①-②得,an=-
an+
an-1,
即
an=
an-1,
∴
=
(n≥2),
∴数列{
}是以
为首项,以
为公比的等比数列;
∵数列{
}是以
为首项,以
为公比的等比数列,
∴
=
,an=
.
则2nan=2n•
=n.
∴Tn=1+2+3+…+n=
.
则
=
=2(
-
).
故An=2(1-
+
-
+
-
+…+
-
)=2(1-
)=
.
| 2 |
| n |
取n=1,得a1=S1=2-(2+1)a1,即a1=
| 1 |
| 2 |
当n≥2时,Sn-1=2-(
| 2 |
| n-1 |
①-②得,an=-
| n+2 |
| n |
| n+1 |
| n-1 |
即
| 2n+2 |
| n |
| n+1 |
| n-1 |
∴
| an |
| n |
| 1 |
| 2 |
| an-1 |
| n-1 |
∴数列{
| an |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
∵数列{
| an |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| an |
| n |
| 1 |
| 2n |
| n |
| 2n |
则2nan=2n•
| n |
| 2n |
∴Tn=1+2+3+…+n=
| n(n+1) |
| 2 |
则
| 1 |
| Tn |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
故An=2(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 2n |
| n+1 |
点评:本题考查了等比关系的确定,考查了等差数列的前n项和,训练了裂项相消法求数列的前n项和,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在平面直角坐标系xOy中,P是直线2x+2y-1=0上的一点,Q是射线OP上的一点,满足|OP|•|OQ|=1.
(Ⅰ)求Q点的轨迹;
(Ⅱ)设点M(x,y)是(Ⅰ)中轨迹上任意一点,求x+7y的最大值.
(Ⅰ)求Q点的轨迹;
(Ⅱ)设点M(x,y)是(Ⅰ)中轨迹上任意一点,求x+7y的最大值.
在平面直角坐标系xOy中,设点M与曲线Ci上任意一点距离的最小值为di(i=1,2),若d1<d2,则称C1比C2更靠近点M,下列为假命题的是( )
| A、C1:x=0比C2:y=0更靠近M(1,-2) |
| B、C1:y=ex比C2:xy=1更靠近M(0,0) |
| C、若C1:(x-2)2+y2=1比C2:x2+(y-2)2=1更靠近点M(m,2m),则m>0 |
| D、若m>1,则C1:y2=4x比C2:x-y+m=0更靠近点M(1,0) |
已知双曲线
-
=1的右焦点到其渐近线的距离等于
,则该双曲线的离心率等于( )
| x2 |
| 4 |
| y2 |
| m2 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
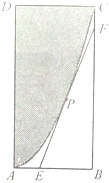 如图,有一个长方形地块ABCD,边AB为2km,AD为4km.,地块的一角是湿地(图中阴影部分),其边缘线AC是以直线AD为对称轴,以A为顶点的抛物线的一部分.现要铺设一条过边缘线AC上一点P的直线型隔离带EF,E,F分别在边AB,BC上(隔离带不能穿越湿地,且占地面积忽略不计).设点P到边AD的距离为t(单位:km),△BEF的面积为S(单位:km2).
如图,有一个长方形地块ABCD,边AB为2km,AD为4km.,地块的一角是湿地(图中阴影部分),其边缘线AC是以直线AD为对称轴,以A为顶点的抛物线的一部分.现要铺设一条过边缘线AC上一点P的直线型隔离带EF,E,F分别在边AB,BC上(隔离带不能穿越湿地,且占地面积忽略不计).设点P到边AD的距离为t(单位:km),△BEF的面积为S(单位:km2).