题目内容
在平面直角坐标系xOy中,P是直线2x+2y-1=0上的一点,Q是射线OP上的一点,满足|OP|•|OQ|=1.
(Ⅰ)求Q点的轨迹;
(Ⅱ)设点M(x,y)是(Ⅰ)中轨迹上任意一点,求x+7y的最大值.
(Ⅰ)求Q点的轨迹;
(Ⅱ)设点M(x,y)是(Ⅰ)中轨迹上任意一点,求x+7y的最大值.
考点:简单曲线的极坐标方程,轨迹方程
专题:计算题,坐标系和参数方程
分析:(Ⅰ)设射线OP的极坐标方程为ρ=
,依题意可知,动点Q的极坐标为(ρ,θ),P(ρ′,a),由|OP|•|OQ|=1,可得ρ′•ρ=1,即可求出Q点的轨迹;
(Ⅱ)设M(1+
cosα,1+
sinα),可得x+7y=1+
cosα+7+7
sinα=8+10sin(α+γ),即可求x+7y的最大值.
| 1 |
| 2cosθ+2sinθ |
(Ⅱ)设M(1+
| 2 |
| 2 |
| 2 |
| 2 |
解答:
解:(Ⅰ)设射线OP的极坐标方程为ρ=
,
依题意可知,动点Q的极坐标为(ρ,θ),P(ρ′,a),由|OP|•|OQ|=1,可得ρ′•ρ=1.
∴ρ=
=2cosθ+2sinθ,
∴ρ2=2ρcosθ+2ρsinθ,
∴x2+y2=2x+2y,
∴(x-1)2+(y-1)2=2,
∴Q点的轨迹是以(1,1)为圆心,
为半径的圆;
(Ⅱ)设M(1+
cosα,1+
sinα),
∴x+7y=1+
cosα+7+7
sinα=8+10sin(α+γ),
∴x+7y的最大值为18.
| 1 |
| 2cosθ+2sinθ |
依题意可知,动点Q的极坐标为(ρ,θ),P(ρ′,a),由|OP|•|OQ|=1,可得ρ′•ρ=1.
∴ρ=
| 1 |
| ρ′ |
∴ρ2=2ρcosθ+2ρsinθ,
∴x2+y2=2x+2y,
∴(x-1)2+(y-1)2=2,
∴Q点的轨迹是以(1,1)为圆心,
| 2 |
(Ⅱ)设M(1+
| 2 |
| 2 |
∴x+7y=1+
| 2 |
| 2 |
∴x+7y的最大值为18.
点评:本题考查极坐标与参数方程,考查轨迹方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知集合M={-1,1,2},N={x∈R|x2-5x+4=0},则M∪N=( )
| A、ϕ | B、{1} |
| C、{1,4} | D、{-1,1,2,4} |
“所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数”,上述推理( )
| A、推理形式不正确 |
| B、大前提错误 |
| C、错误,因为大小前提不一致 |
| D、完全正确 |
甲、乙两人从4门课程中各选修2门,则甲、乙两人所选的课程中有一门相同的选法有( )
| A、6种 | B、12种 |
| C、16种 | D、24 |
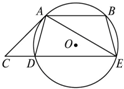 如图,四边形ABED内接于⊙O,AB∥DE,AC切⊙O于A,交ED延长线于C.若AD=BE=
如图,四边形ABED内接于⊙O,AB∥DE,AC切⊙O于A,交ED延长线于C.若AD=BE=