题目内容
已知函数f(x)=x2-2x+a(x∈[0,3]),它的任意三个函数值总可以作为一个三角形的三边长,则a的取值范围是 .
考点:二次函数的性质
专题:函数的性质及应用
分析:解析:利用二次函数的对称轴x=1,求出函数f(x)max=f(3)=3+a,f(x)min=f(1)=a-1,所以
进一步解得a的取值范围.
|
解答:
解:已知函数f(x)=x2-2x+a(x∈[0,3]),
所以:函数是开口方向向上,对称轴为x=1的抛物线.
f(x)max=f(3)=3+a,
f(x)min=f(1)=a-1,
它的任意三个函数值总可以作为一个三角形的三边长,
所以
解得a∈(5,+∞).
故答案为:(5,+∞).
所以:函数是开口方向向上,对称轴为x=1的抛物线.
f(x)max=f(3)=3+a,
f(x)min=f(1)=a-1,
它的任意三个函数值总可以作为一个三角形的三边长,
所以
|
解得a∈(5,+∞).
故答案为:(5,+∞).
点评:本题考查的知识要点:二次函数的性质的应用.三角形的三边关系的应用.属于基础题型.

练习册系列答案
相关题目
设点P(m,n)(n≠0)是角为600°的终边上的一点,则
的值为( )
| n |
| m |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
若复数z1=5+13i,z2=7+28i,其中i是虚数单位,则复数(z1-z2)i的实部为 (
| A、-20 | B、15 | C、30 | D、8 |
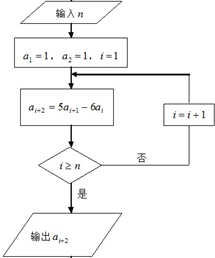 已知数列{an}满足如图所示的程序框图.
已知数列{an}满足如图所示的程序框图.