Question

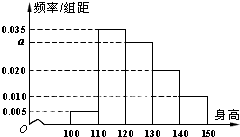从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．由图中数据可知a=

 

．若要从身高在[120，130），[130，140），[140，150），三组内的学生中，用分层抽样的方法选取12人参加一项活动，则从身高在[140，150）内的学生中选取的人数应为

 

．

Answer 1

考点：频率分布直方图

专题：概率与统计

分析：根据频率分布直方图中各小长方形的面积之和为1，求出a的值；根据分层抽样原理求出从身高在[140，150）内的学生中选取的人数．

解答： 解：根据频率分布直方图，各小长方形的面积之和为1，得
（0.005+0.035+a+0.020+0.010）×10=1，
∴a=0.030；
根据分层抽样方法知，从身高在[140，150）内的学生中选取的人数应为
12×

0.010

0.030+0.020+0.010

=2；
故答案为：0.030、2．

点评：本题考查了频率分布直方图以及分层抽样方法的应用问题，解题时应根据频率分布直方图中各小长方形的面积之和为1以及分层抽样原理求出答案．