题目内容
已知函数f(x)=
,x∈R,则f(
)=( )
| 1 |
| x2+1 |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:函数的值
专题:函数的性质及应用
分析:利用函数的性质求解.
解答:
解:函数f(x)=
,x∈R,
∴f(
)=
=
.
故选:D.
| 1 |
| x2+1 |
∴f(
| 1 |
| 2 |
| 1 | ||
|
| 4 |
| 5 |
故选:D.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
设函数f(x)=
,若f(a)=4,则实数a=( )
|
| A、-4或2 | B、-4或-2 |
| C、-2或4 | D、-2或2 |
使函数y=2sin(3x+φ)+2
cos(3x+φ)为奇函数,且在[0,
]上是减函数的一个φ值是( )
| 3 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=x+
,则对任意不为零的实数x恒成立的是( )
| 1 |
| x |
| A、f(x)=f(-x) | ||
B、f(x)=f(
| ||
C、f(x)=-f(
| ||
D、f(x)f(
|
下列各图形中,不可能是函数图象的是( )
A、 |
B、 |
C、 |
D、 |
函数y=sin(2x-
)的图象可由函数y=sin2x的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知α,β∈(0,
),满足tan(α+β)=4tanβ,则tanα的最大值是.
| π |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
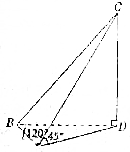 如图,A,B是海平面上的两个点,相距800m,在A点测得山顶C的仰角为45°,∠BAD=120°,又在B点测得∠ABD=45°,其中D是点C到水平面的射线,则山高CD=
如图,A,B是海平面上的两个点,相距800m,在A点测得山顶C的仰角为45°,∠BAD=120°,又在B点测得∠ABD=45°,其中D是点C到水平面的射线,则山高CD=