题目内容
11. 如图所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是侧面ABB'A'的中心,点D、E、F分别是棱A'C'、AB、BB'的中点.
如图所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是侧面ABB'A'的中心,点D、E、F分别是棱A'C'、AB、BB'的中点.(1)证明OD∥平面BCC'B';
(2)求直线EF和AC所成的角.
分析 (1)侧面AA′B′B为正方形,连结A′B,则O为A′B的中点,从而OD∥BC′,由此能证明OD∥平面BCC'B'.
(2)取BC中点M,连结EM、FM,则∠FEM为异面直线EF与AC所成的角,由此能求出直线EF和AC所成的角.
解答 证明:(1)依题意可知侧面AA′B′B为正方形,连结A′B,则O为A′B的中点,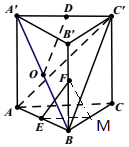 在△A′BC′中,O、D分别是边A′B、A′C′的中点,
在△A′BC′中,O、D分别是边A′B、A′C′的中点,
∴OD∥BC′,
∵BC′?平面BCC'B',OD?平面BCC'B',
∴OD∥平面BCC'B'.
解:(2)取BC中点M,连结EM、FM,
则∠FEM为异面直线EF与AC所成的角,
设AB=2,则EM=EF=FM=$\sqrt{2}$,∴∠FEM=60°,
∴直线EF和AC所成的角为60°.
点评 本题考查线面平行的证明,考查异面直线所成角的求法,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力,是中档题.

练习册系列答案
相关题目
16.执行如图所示的语句,结果为( )


| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
3.已知点(2,0)到双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线的距离为$\sqrt{3}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{10}}}{3}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
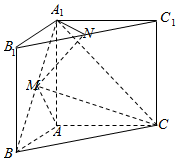 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.