题目内容
19.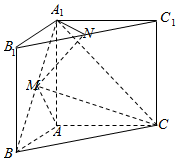 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,点M,N分别为A1B 和B1C1的中点.(1)证明:MN∥平面A1ACC1
(2)证明:A1M⊥平面MAC.
分析 (1)取A1B1的中点D,连结MD、ND,推导出DM∥AA1,DN∥A1C1,从而平面DMN∥平面A1ACC1,由此能证明MN∥平面A1ACC1.
(2)推导出AM⊥A1B,由余弦定理得AC=2$\sqrt{3}$,从而${A}_{1}C=\sqrt{A{{A}_{1}}^{2}+A{C}^{2}}$=4,进而CM⊥A1B,由此能证明A1M⊥平面MAC.
解答 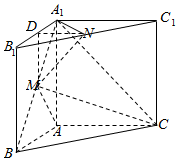 证明:(1)取A1B1的中点D,连结MD、ND,
证明:(1)取A1B1的中点D,连结MD、ND,
∵在三棱柱ABC-A1B1C1中,侧棱与底面垂直,点M,N分别为A1B 和B1C1的中点,
∴DM∥AA1,DN∥A1C1,
∵DM∩DN=D,AA1∩A1C1=A1,
DM,DN?平面DMN,AA1,A1C1?平面A1ACC1,
∴平面DMN∥平面A1ACC1,
∵MN?平面DMN,∴MN∥平面A1ACC1.
(2)∵侧棱与底面垂直,AB=AA1=2,∠ABC=60°,BC=4,
点M,N分别为A1B 和B1C1的中点,
∴AM⊥A1B,AC=$\sqrt{{2}^{2}+{4}^{2}-2×2×4×cos60°}$=2$\sqrt{3}$,
${A}_{1}C=\sqrt{A{{A}_{1}}^{2}+A{C}^{2}}$=$\sqrt{4+12}$=4,∴CM⊥A1B,
∵AM∩CM=M,∴A1M⊥平面MAC.
点评 本题考查线面平行的证明,考查线面垂直的证明,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
10.如果a>b,则下列不等式正确的是( )
| A. | $\frac{1}{a}>\frac{1}{b}$ | B. | 2a>2b | C. | |a|>|b| | D. | a2>b2 |
4.设函数$f(x)=3sin(ωx+\frac{π}{6}),ω>0,x∈R$的最小正周期为$\frac{π}{2}$.
(1)求f(x)的解析式;
(2)利用“五点作图法”,画出f(x)在长度为一个周期的闭区间上的简图;

(3)已知$f(\frac{α}{4}+\frac{π}{12})=\frac{9}{5}$,求cosα的值.
(1)求f(x)的解析式;
(2)利用“五点作图法”,画出f(x)在长度为一个周期的闭区间上的简图;
| ωx+$\frac{π}{6}$ | |||||
| x | |||||
| f(x) |

(3)已知$f(\frac{α}{4}+\frac{π}{12})=\frac{9}{5}$,求cosα的值.
8.已知a=2${\;}^{-\frac{1}{3}}$,b=log${\;}_{\frac{1}{4}}$3,c=log25,则( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
9.从装有3个黑球和3个白球(大小、形状相同)的盒子中随机摸出3个球,用ξ表示摸出的黑球个数,则P(ξ≥2)的值为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
 如图所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是侧面ABB'A'的中心,点D、E、F分别是棱A'C'、AB、BB'的中点.
如图所示,在三棱柱ABC-A'B'C'中,AA'⊥底面ABC,AB=BC=AA',∠ABC=90°,O是侧面ABB'A'的中心,点D、E、F分别是棱A'C'、AB、BB'的中点.