题目内容
(Ⅰ)已知a是实数,i是虚数单位,
是纯虚数,求a的值;
(Ⅱ)设z=
,求|z|.
| (a-i)(1-i) |
| i |
(Ⅱ)设z=
| (1-4i)(1+i)+2+4i |
| 3+4i |
考点:复数求模,复数的基本概念,复数代数形式的乘除运算
专题:计算题,数系的扩充和复数
分析:(Ⅰ)先化简
,由纯虚数的定义可求a值;
(Ⅱ)先化简z,然后可求模;
| (a-i)(1-i) |
| i |
(Ⅱ)先化简z,然后可求模;
解答:
解:(Ⅰ)
=
=-(a+1)+(1-a)i,
∵
是纯虚数,
∴-(a+1)=0,1-a≠0,即a=-1;
(Ⅱ)z=
=
=
=
=1-i,
|z|=
=
.
| (a-i)(1-i) |
| i |
| (a-i)(1-i)(-i) |
| i(-i) |
∵
| (a-i)(1-i) |
| i |
∴-(a+1)=0,1-a≠0,即a=-1;
(Ⅱ)z=
| (1-4i)(1+i)+2+4i |
| 3+4i |
| 7+i |
| 3+4i |
| (7+i)(3-4i) |
| (3+4i)(3-4i) |
| 25-25i |
| 25 |
|z|=
| 12+(-1)2 |
| 2 |
点评:该题考查复数代数形式的乘除运算、复数的基本概念,属基础题.

练习册系列答案
相关题目
与直线3x+4y-5=0关于x轴对称的直线的方程为( )
| A、3x-4y+5=0 |
| B、3x+4y-5=0 |
| C、4x+3y-5=0 |
| D、4x+3y+5=0 |
求值:sin12°cos18°+cos12°sin18°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
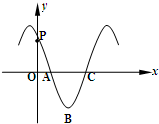 函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中点P为y=f′(x)的图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中点P为y=f′(x)的图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.