题目内容
已知函数f(x)=alnx-x.
(1)当a=1时,求f(x)的极值;
(2)若f(x)≤a对x∈[1,+∞]恒成立,求实数a的取值范围.
(1)当a=1时,求f(x)的极值;
(2)若f(x)≤a对x∈[1,+∞]恒成立,求实数a的取值范围.
考点:利用导数研究函数的极值,函数恒成立问题
专题:导数的综合应用
分析:(1)由f(x)=lnx-x,得f′(x)=
-1;令f′(x)=0,解得:x=1.从而求出函数的单调区间,进而得到f(x)的极大值f(1)=-1.
(2)先求出函数的导函数为:f′(x)=
-1=
,x∈[1,+∞),再分别讨论①当a≤0时,②当a>0时的情况,从而综合得出结论.
| 1 |
| x |
(2)先求出函数的导函数为:f′(x)=
| a |
| x |
| a-x |
| x |
解答:
解:(1)∵f(x)=lnx-x,
∴f′(x)=
-1;
令f′(x)=0,
解得:x=1.
当x∈(0,1)时,f′(x)>0,
∴f(x)是增函数;
当x∈(1,+∞)时,f′(x)<0,
∴f(x)是减函数.
∴f(x)的极大值f(1)=-1.
(2)f′(x)=
-1=
,x∈[1,+∞),
①当a≤0时,f′(x)<0,
∴f(x)是减函数,即f(x)≤f(1)=-1,
∴-1≤a≤0;
②当a>0时,当x∈(0,a)时,f′(x)>0,
∴f(x)是增函数;
当x∈(a,+∞)时,f′(x)<0,
∴f(x)是减函数.
(ⅰ)当0<a≤1时,在x∈[1,+∞)时f(x)是减函数,即f(x)≤f(1)=-1,
∴0<a≤1;
(ⅱ) 当a>1时,当x∈(1,a)时,f′(x)>0,
∴f(x)是增函数;
当x∈(a,+∞)时,f′(x)<0,
∴f(x)是减函数.
∴f(x)≤f(a)=alna-a,
即alna-a≤a,
∴1<a≤e2,
综上:-1≤a≤e2.
∴f′(x)=
| 1 |
| x |
令f′(x)=0,
解得:x=1.
当x∈(0,1)时,f′(x)>0,
∴f(x)是增函数;
当x∈(1,+∞)时,f′(x)<0,
∴f(x)是减函数.
∴f(x)的极大值f(1)=-1.
(2)f′(x)=
| a |
| x |
| a-x |
| x |
①当a≤0时,f′(x)<0,
∴f(x)是减函数,即f(x)≤f(1)=-1,
∴-1≤a≤0;
②当a>0时,当x∈(0,a)时,f′(x)>0,
∴f(x)是增函数;
当x∈(a,+∞)时,f′(x)<0,
∴f(x)是减函数.
(ⅰ)当0<a≤1时,在x∈[1,+∞)时f(x)是减函数,即f(x)≤f(1)=-1,
∴0<a≤1;
(ⅱ) 当a>1时,当x∈(1,a)时,f′(x)>0,
∴f(x)是增函数;
当x∈(a,+∞)时,f′(x)<0,
∴f(x)是减函数.
∴f(x)≤f(a)=alna-a,
即alna-a≤a,
∴1<a≤e2,
综上:-1≤a≤e2.
点评:本题考察了函数的单调性,函数的极值问题,函数的恒成立问题,渗透了分类讨论思想,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
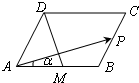 在平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,点M为AB的中点,点P从B→C→D(含端点),设∠PAB=α,记tanα=x,
在平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,点M为AB的中点,点P从B→C→D(含端点),设∠PAB=α,记tanα=x,| AP |
| DM |
A、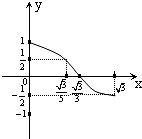 |
B、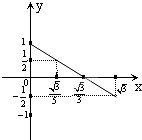 |
C、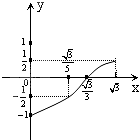 |
D、 |
若θ为锐角且cosθ-cos-1θ=-2,则cosθ+cos-1θ的值为( )
A、2
| ||
B、
| ||
| C、6 | ||
| D、4 |
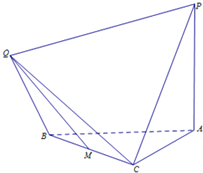 如图,多面体ABCPQ中,PA⊥平面ABC,PA=AB,△ABC是等腰直角三角形,∠BAC=90°,△QBC是等边三角形,M是BC的中点,二面角Q-BC-A的正切值为-
如图,多面体ABCPQ中,PA⊥平面ABC,PA=AB,△ABC是等腰直角三角形,∠BAC=90°,△QBC是等边三角形,M是BC的中点,二面角Q-BC-A的正切值为-