题目内容
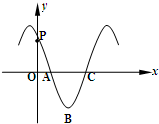 函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中点P为y=f′(x)的图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,其中点P为y=f′(x)的图象与y轴的交点,A,C为图象与x轴的两个交点,B为图象的最低点.(1)求曲线段
 |
| ABC |
(2)若|AC|=
| π |
| 3 |
3
| ||
| 2 |
| π |
| 2 |
| π |
| 3 |
考点:导数的运算
专题:导数的综合应用,三角函数的图像与性质
分析:(1)利用定积分的意义可得:曲线段
与x轴所围成的区域的面积S=|
f′(x)dx|.
(2)由图象可知:|AC|=
=
=
,解得ω=3.由点P的坐标为(0,
),代入可得φ=
.即可得出f(x)=sin(3x+
).再利用当x∈[0,
]时,
≤3x+
≤
,即可得出.
 |
| ABC |
| ∫ | c a |
(2)由图象可知:|AC|=
| T |
| 2 |
| ||
| 2 |
| π |
| 3 |
3
| ||
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
解答:
解:(1)曲线段
与x轴所围成的区域的面积S=|
f′(x)dx|=|f(x)
|=|sin(ωc+φ)-sin(ωa+φ)|=2.
(2)由图象可知:|AC|=
=
=
=
,解得ω=3.
∵点P的坐标为(0,
),
∴3cosφ=
,0<φ<
,解得φ=
.
∴f(x)=sin(3x+
).
当x∈[0,
]时,
≤3x+
≤
,
∴-
≤sin(3x+
)≤1
 |
| ABC |
| ∫ | c a |
| | | c a |
(2)由图象可知:|AC|=
| T |
| 2 |
| ||
| 2 |
| π |
| ω |
| π |
| 3 |
∵点P的坐标为(0,
3
| ||
| 2 |
∴3cosφ=
3
| ||
| 2 |
| π |
| 2 |
| π |
| 6 |
∴f(x)=sin(3x+
| π |
| 6 |
当x∈[0,
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
点评:本题考查了三角函数的图象与性质、定积分的几何意义,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
若θ为锐角且cosθ-cos-1θ=-2,则cosθ+cos-1θ的值为( )
A、2
| ||
B、
| ||
| C、6 | ||
| D、4 |
 如图所示,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰直角三角形,
如图所示,四棱锥P-ABCD的底面ABCD是矩形,侧面PAD是等腰直角三角形,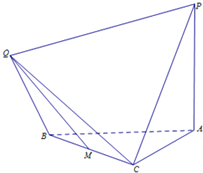 如图,多面体ABCPQ中,PA⊥平面ABC,PA=AB,△ABC是等腰直角三角形,∠BAC=90°,△QBC是等边三角形,M是BC的中点,二面角Q-BC-A的正切值为-
如图,多面体ABCPQ中,PA⊥平面ABC,PA=AB,△ABC是等腰直角三角形,∠BAC=90°,△QBC是等边三角形,M是BC的中点,二面角Q-BC-A的正切值为- 如图所示,四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,则AC1=
如图所示,四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AD=3,AA1=5,∠BAA1=∠DAA1=60°,则AC1=