题目内容
函数f（x）=x2+14x-3在区间（-5，5）上最大值、最小值情况为（ ）
| A、有最大值，没最小值 |
| B、有最小值，没最大值 |
| C、有最大值，也有最小值 |
| D、没有最大值，也没有最小值 |
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：利用配方法将二次函数进行配方，即可得到函数的最值情况．
解答：
解：∵f（x）=x2+14x-3=（x+7）-52，
∴对称轴为x=-7，抛物线开口向上，
∴函数f（x）在（-5，5）单调递增，
∴函数无最大值和最小值．
故选：D．
∴对称轴为x=-7，抛物线开口向上，
∴函数f（x）在（-5，5）单调递增，
∴函数无最大值和最小值．
故选：D．
点评：本题主要考查二次函数的图象和性质，利用配方法确定二次函数的对称轴是解决本题的关键．
练习册系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
设a，b，c∈R，且a＜b，则（ ）
| A、ac＞bc | ||||
B、
| ||||
| C、a2＞b2 | ||||
| D、a3＜b3 |
已知直线l的斜率为k（k≠0），它在x轴、y轴上的截距分别为k、2k，则直线l的方程为（ ）
| A、2x-y-4=0 |
| B、2x-y+4=0 |
| C、2x+y-4=0 |
| D、2x+y+4=0 |
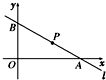已知直线l过点P（3，2），且与x轴、y轴的正半轴分别交于A，B两点，如图所示，则△ABO的面积的最小值为（ ）| A、6 | B、12 | C、24 | D、18 |
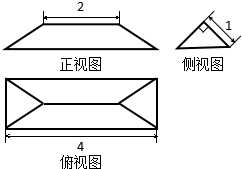如图所示，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等腰梯形，等腰直角三角形和长方形，则该几何体体积为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|