题目内容
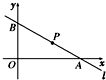已知直线l过点P（3，2），且与x轴、y轴的正半轴分别交于A，B两点，如图所示，则△ABO的面积的最小值为（ ）| A、6 | B、12 | C、24 | D、18 |
考点：直线的截距式方程
专题：直线与圆
分析：设出直线方程的截距式，代入P得坐标，然后利用基本不等式求得ab的最小值，则△ABO的面积的最小值可求．
解答：
解：直线l与x轴，y轴正半轴分别交于A，B两点，
设直线方程为：
+
=1 （a＞0，b＞0），
∵直线l过点P（3，2），
则：
+
=1，
由1=
+
≥2
，
得：ab≥24，
∴△ABO面积S=
ab≥12，当且仅当
=
，即a=6，b=4时取等号．
故选：B．
设直线方程为：
| x |
| a |
| y |
| b |
∵直线l过点P（3，2），
则：
| 3 |
| a |
| 2 |
| b |
由1=
| 3 |
| a |
| 2 |
| b |
|
得：ab≥24，
∴△ABO面积S=
| 1 |
| 2 |
| 3 |
| a |
| 2 |
| b |
故选：B．
点评：本题考查了直线的截距式方程，考查了利用基本不等式求最值，是中低档题．
练习册系列答案
相关题目
函数f(x)=log2sin(
-
)的单调递增区间是（ ）
| π |
| 3 |
| x |
| 2 |
A、(4kπ-
| ||||
B、(4kπ-
| ||||
C、(4kπ-
| ||||
D、(2kπ-
|
若不论m取何实数，直线l：mx+y-1+2m=0恒过一定点，则该定点的坐标为（ ）
| A、（-2，1） |
| B、（2，-1） |
| C、（-2，-1） |
| D、（2，1） |
函数f（x）=x2+14x-3在区间（-5，5）上最大值、最小值情况为（ ）
| A、有最大值，没最小值 |
| B、有最小值，没最大值 |
| C、有最大值，也有最小值 |
| D、没有最大值，也没有最小值 |
圆x2+y2=2截直线x-y-1=0所得弦长为（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|