题目内容
若2|log2a|=
,则a的取值范围为 .
| 1 |
| a |
考点:指数函数的图像与性质
专题:函数的性质及应用
分析:讨论a的取值范围,利用指数恒等式和对数的基本运算公式进行计算即可.
解答:
解:若0<a<1,则等式2|log2a|=
,等价为2-log2a=2log2
=
=
,此时等式恒成立.
若a=1,则等式2|log2a|=
,等价为20=
,此时等式恒成立.
若a>1,则等式2|log2a|=
,等价为2log2a=a=
,解得a=1,此时等式不成立.
综上:0<a≤1,
故答案为:0<a≤1
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
若a=1,则等式2|log2a|=
| 1 |
| a |
| 1 |
| 1 |
若a>1,则等式2|log2a|=
| 1 |
| a |
| 1 |
| a |
综上:0<a≤1,
故答案为:0<a≤1
点评:本题主要考查指数方程的解法,根据对数的运算性质和指数恒等式是解决本题的关键,注意要对a进行分类讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
直线2kx+y-6k+1=0(k∈R)经过定点P,则P为( )
| A、(1,3) |
| B、(3,1) |
| C、(-1,-3) |
| D、(3,-1) |
以初速度40m/s竖直向上抛一物体,t秒时刻的速度v=40-10t2,则此物体达到最高时的高度为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=x2+14x-3在区间(-5,5)上最大值、最小值情况为( )
| A、有最大值,没最小值 |
| B、有最小值,没最大值 |
| C、有最大值,也有最小值 |
| D、没有最大值,也没有最小值 |
在△ABC中,A=60°,a=4
,b=4
,则B=( )
| 3 |
| 2 |
| A、30° | B、45° |
| C、120° | D、135° |
设f(x)=ex+x-4,则函数f(x)=0的解位于区间( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
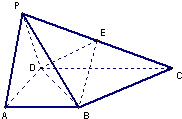 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB,平面PAD⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB,平面PAD⊥底面ABCD,E是PC的中点.