题目内容
10.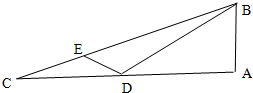 如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.
如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.
分析 经E点作EF⊥AC于F点,设AB=x,则由题意可求得BD,AD,AC,BC2,EF,ED,△EDB中,由余弦定理,整理可得:5x2-8$\sqrt{3}$x-12=0,可解得x,从而可求BC.
解答 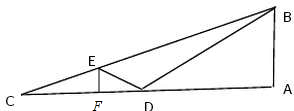
解:如图,经E点作EF⊥AC于F点,设AB=x,则由题意可得,
BD=2x,AD=$\sqrt{3}$x,AC=3+$\sqrt{3}$x,BC2=x2+(3+$\sqrt{3}$x)2,
∵△CEF∽△ABC,∴$\frac{EF}{AB}=\frac{EC}{BC}$=$\frac{1}{5}$,即有EF=$\frac{1}{5}$x,
∵∠BDE=120°,AB=$\frac{1}{2}$BD,
∴∠EDF=30°,∴ED=2EF=$\frac{2}{5}$x,
∴△EDB中,由余弦定理知:BE2=DE2+BD2-2ED×BD×cos120°
=$\frac{4}{25}$x2+4x2-2×$\frac{2}{5}$x×2x×(-$\frac{1}{2}$)=$\frac{16}{25}$BC2
=$\frac{16}{25}$[x2+(3+$\sqrt{3}$x)2],
整理可得:5x2-8$\sqrt{3}$x-12=0,
∴可解得:x=2$\sqrt{3}$或-$\frac{2\sqrt{3}}{5}$(舍去),
∴BC2=x2+(3+$\sqrt{3}$x)2=93,可解得:BC=$\sqrt{93}$.
故答案为:$\sqrt{93}$.
点评 本题主要考察了余弦定理的应用,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
8.已知点A($\sqrt{3}$,0)和P($\sqrt{3}$,t)(t∈R).若曲线x=$\sqrt{3-{y}^{2}}$上存在点B使∠APB=60°,则t的取值范围是( )
| A. | (0,1+$\sqrt{3}$] | B. | [0,1+$\sqrt{3}$] | C. | [-1-$\sqrt{3}$,1+$\sqrt{3}$] | D. | [-1-$\sqrt{3}$,0)∪(0,1+$\sqrt{3}$] |
1.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的单调递增区间为( )
| A. | [kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$]k∈Z | B. | [kπ+$\frac{5π}{12}$,kπ+$\frac{11π}{12}$]k∈Z | ||
| C. | [kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$]k∈Z | D. | [kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$]k∈Z |
18.函数f(x)=ax2+bx+2a-b是定义在[a-1,2a]上的偶函数,则a+b=( )
| A. | -$\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | 0 | D. | 1 |
5.已知x、y满足约束条件$\left\{\begin{array}{l}{x-y≥1}\\{2x-y+1≤0}\end{array}\right.$,且目标函数z=mx-ny(m>0,n<0)的最大值为-6,则$\frac{n}{m-1}$的取值范围是( )
| A. | [-2,0]∪[$\frac{1}{2}$,+∞) | B. | [2,+∞) | C. | (-∞,0)∪(2,+∞) | D. | (-∞,0)∪[$\frac{1}{2}$,+∞) |
2.“若x2=1,则x=1”的否命题为( )
| A. | 若x2≠1,则x=1 | B. | 若x2=1,则x≠1 | C. | 若x2≠1,则x≠1 | D. | 若x≠1,则x2≠1 |
19.若函数f(x)=$\frac{1}{3}$x3-(a+$\frac{1}{2}$)x2+(a2+a)x-$\frac{1}{2}$a2+$\frac{1}{2}$有两个以上的零点,则a的取值范围是( )
| A. | (-2,-1) | B. | (-∞,-2)∪(-1,+∞) | C. | $(-\root{3}{{\frac{3}{2}}},-1)$ | D. | $(-∞,-\root{3}{{\frac{3}{2}}})∪(-1,+∞)$ |