题目内容
20.在△ABC中,点D在BC边上,AD平分∠BAC,AB=6,AD=3$\sqrt{2}$,AC=4.(1)利用正弦定理证明:$\frac{AB}{AC}=\frac{BD}{DC}$;
(2)求BC的长.
分析 (1)由正弦定理知$\frac{AB}{sin∠ADB}=\frac{BD}{sin∠BAD}$,$\frac{AC}{sin∠ADC}=\frac{DC}{sin∠DAC}$,由已知及诱导公式可得sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC,由①÷②即可得证.
(2)由(1)知,$\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{2}$,设BD=3x,DC=2x(x>0),则BC=5x,由cos∠BDA+cos∠ADC=0及余弦定理即可解得x的值,从而得解.
解答  解:(1)证明:由正弦定理知,在△ABD中,$\frac{AB}{sin∠ADB}=\frac{BD}{sin∠BAD}$;
解:(1)证明:由正弦定理知,在△ABD中,$\frac{AB}{sin∠ADB}=\frac{BD}{sin∠BAD}$;
在△ADC中,$\frac{AC}{sin∠ADC}=\frac{DC}{sin∠DAC}$,
由∠ADB+∠ADC=π,∠BAD=∠DAC,
得sin∠ADB=sin∠ADC,sin∠BAD=sin∠DAC.
由①÷②得:$\frac{AB}{AC}=\frac{BD}{DC}$.
(2)由(1)知,$\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{2}$,
设BD=3x,DC=2x(x>0),
则BC=5x,
由cos∠BDA+cos∠ADC=0及余弦定理知,$\frac{{9{x^2}+18-36}}{{18\sqrt{2}x}}+\frac{{4{x^2}+18-16}}{{12\sqrt{2}x}}=0$,
解得x=1,
所以BC=5.
点评 本题主要考查了正弦定理,诱导公式,余弦定理在解三角形中的综合应用,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
相关题目
9.已知等差数列{an}的前7项和为14,则${e^{a_2}}•{e^{a_3}}•{e^{a_5}}•{e^{a_6}}$=( )
| A. | e2 | B. | e4 | C. | e8 | D. | e16 |
10.△ABC的三边长分别是a,b,c,且a=1,B=45°,S△ABC=2,则△ABC的外接圆的面积为( )
| A. | 25π | B. | 5π | C. | $\frac{25π}{2}$ | D. | $\frac{5π}{2}$ |
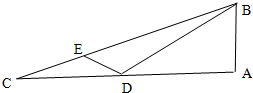 如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.
如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.