题目内容
15.已知函数y=sinx(x∈[0,π])图象上两个点A(x1,y1),B(x2,y2)(x1<x2)满足AB∥x轴,O是坐标原点,若点C的坐标为(π,0),则四边形OABC的面积最大时,tanx1-x2=0.分析 根据题意,求出四边形OABC的面积S四边形OABC取最大值时x1+tanx1=π,再由y1=y2,得出A与B关于x=$\frac{π}{2}$对称,x2+x1=π,即可得出tanx1-x2=0.
解答 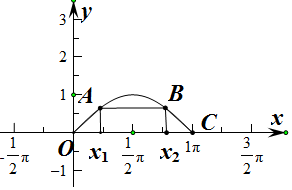 解:∵x∈[0,π],
解:∵x∈[0,π],
∴y1=y2>0,
∴S梯形OABC=$\frac{1}{2}$(AB+OC)•y1
=$\frac{1}{2}$[(x2-x1)+π]•sinx1,
∵A与B关于x=$\frac{π}{2}$对称,∴$\frac{1}{2}$(x2+x1)=$\frac{π}{2}$,
∴x2=π-x1,
∴S梯形=(π-x1)sinx1,x1∈(0,$\frac{π}{2}$),
令y=(π-x)sinx,
∴y′=-sinx+(π-x)cosx=0,
∴tanx=π-x,
∴tanx+x=π,
∴y的最大值处有tanx+x=π,
∴x1+tanx1=π,
∴tanx1-x2=(π-x1)-(π-x1)=0.
故答案为:0.
点评 本题考查了三角函数的图象与性质的应用问题,也考查了四边形面积的计算问题,是较难的题目.

练习册系列答案
相关题目
20.设函数f(x)是定义在R上的偶函数,f'(x)为其导函数.当x>0时,f(x)+x•f′(x)>0,且f(1)=0,则不等式x•f(x)>0的解集为( )
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,-1)∪(0,1) | C. | (-1,0)∪(0,1) | D. | (-1,0)∪(1,+∞) |
7.若将函数y=2sin2x的图象向左平移$\frac{π}{12}$个单位得到f(x)的图象,则下列哪项是f(x)的对称中心( )
| A. | $(\frac{π}{12},0)$ | B. | $(\frac{5π}{12},0)$ | C. | $(-\frac{5π}{12},0)$ | D. | $(\frac{π}{6},0)$ |
4.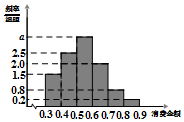 某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
 某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )
某电商对10000名网购者2015年度消费情况进行统计,其消费频率分布直方图如图,则在这些网购者中,消费金额在[0.5,0.9]内的人数为( )| A. | 2000 | B. | 4500 | C. | 6000 | D. | 7500 |
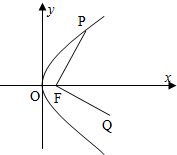 如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$
如图,点P是抛物线y2=4x上动点,F为抛物线的焦点,将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$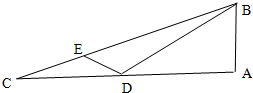 如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.
如图,在Rt△ABC中,∠A=90°,D是AC上一点,E是BC上一点,若AB=$\frac{1}{2}BD,CE=\frac{1}{4}$EB.∠BDE=120°,CD=3,则BC=$\sqrt{93}$.