题目内容
18．函数f（x）=ax2+bx+2a-b是定义在[a-1，2a]上的偶函数，则a+b=（ ）| A． | -$\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | 0 | D． | 1 |
分析 依照偶函数的定义，对定义域内的任意实数，f（-x）=f（x），且定义域关于原点对称，a-1=-2a．
解答 解：∵f（x）=ax2+bx+2a-b是定义在[a-1，2a]上的偶函数，
∴f（-x）=f（x），∴b=0，
又a-1=-2a，
∴a=$\frac{1}{3}$，
∴a+b=$\frac{1}{3}$．
故选：B．
点评 本题考查偶函数的定义，对定义域内的任意实数，f（-x）=f（x）；奇函数和偶函数的定义域必然关于原点对称，定义域区间2个端点互为相反数．
练习册系列答案
教材全解字词句篇系列答案
相关题目
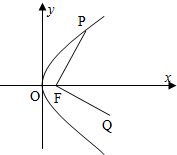如图，点P是抛物线y2=4x上动点，F为抛物线的焦点，将向量$\overrightarrow{FP}$绕点F按顺时针方向旋转90°到$\overrightarrow{FQ}$
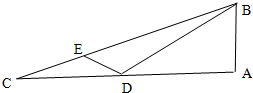如图，在Rt△ABC中，∠A=90°，D是AC上一点，E是BC上一点，若AB=$\frac{1}{2}BD，CE=\frac{1}{4}$EB．∠BDE=120°，CD=3，则BC=$\sqrt{93}$．
7．若将函数y=2sin2x的图象向左平移$\frac{π}{12}$个单位得到f（x）的图象，则下列哪项是f（x）的对称中心（ ）
| A． | $（\frac{π}{12}，0）$ | B． | $（\frac{5π}{12}，0）$ | C． | $（-\frac{5π}{12}，0）$ | D． | $（\frac{π}{6}，0）$ |