题目内容
已知f(x)=cos(
-2x)+2sin2x
(1)若x∈[0,
],求f(x)的值域;
(2)锐角△ABC中,f(C)=
,sinB=
,求cosA.
| π |
| 3 |
(1)若x∈[0,
| π |
| 2 |
(2)锐角△ABC中,f(C)=
| 3 |
| 2 |
| 1 |
| 3 |
考点:三角函数中的恒等变换应用,两角和与差的余弦函数
专题:三角函数的图像与性质
分析:(1)首先通过恒等变换把函数变形成正弦型函数,然后根据定义域进一步确定函数的值域
(2)根据(1)所得的结果进一步确定A、B的正弦值和余弦值,进一步求得结果.
(2)根据(1)所得的结果进一步确定A、B的正弦值和余弦值,进一步求得结果.
解答:
解:(1)已知f(x)=cos(
-2x)+2sin2x=cos
cos2x+sin
sin2x+2
=
sin2x-
cos2x+1=sin(2x-
)+1
∵x∈[0,
]
∴-
≤2x-
≤
∴-
≤sin(2x-
)≤1
∴
≤f(x)≤2
即f(x)的值域为:[
,2]
(2)在锐角△ABC中,
∵f(C)=
∴sin(2C-
)+1=
解得:C=
sinC=
cosC=
∵sinB=
∴cosB=
cosA=-cos(B+C)=
.
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1-cos2x |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
∵x∈[0,
| π |
| 2 |
∴-
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
∴
| 1 |
| 2 |
即f(x)的值域为:[
| 1 |
| 2 |
(2)在锐角△ABC中,
∵f(C)=
| 3 |
| 2 |
∴sin(2C-
| π |
| 6 |
| 3 |
| 2 |
解得:C=
| π |
| 6 |
sinC=
| 1 |
| 2 |
| ||
| 2 |
∵sinB=
| 1 |
| 3 |
∴cosB=
2
| ||
| 3 |
cosA=-cos(B+C)=
1-2
| ||
| 6 |
点评:本题考查的知识点:三角函数的恒等变换,正弦型函数的定义域和值域,三角函数的诱导公式及相关的运算问题.

练习册系列答案
相关题目
已知
,
满足:|
|=2|
|=2
•
=2,若
-
,
-
的夹角为
,则(
•
)max=( )
| a |
| b |
| b |
| a |
| a |
| b |
| c |
| a |
| c |
| b |
| π |
| 2 |
| c |
| a |
A、
| ||||
B、
| ||||
C、1+
| ||||
D、1+
|
一植物园参观路径如图所示,若要全部参观并且路线不重复,则不同的参观路线种数共有( )
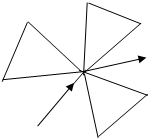

| A、6种 | B、8种 |
| C、36种 | D、48种 |
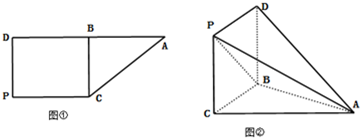
 如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证:
如图所示的四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,E为PC的中点,求证: