题目内容
已知函数f(x)=(x-1)ln(x-1).
(1)设函数g(x)=-a(x-1)+f(x)在区间[2,e2+1]上不单调,求实数a的取值范围;
(2)若k∈Z,且f(x)+x-1-k(x-2)>0对x>2恒成立,求k的最大值.
(1)设函数g(x)=-a(x-1)+f(x)在区间[2,e2+1]上不单调,求实数a的取值范围;
(2)若k∈Z,且f(x)+x-1-k(x-2)>0对x>2恒成立,求k的最大值.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:圆锥曲线的定义、性质与方程
分析:(1)求出函数g(x)=-a(x-1)+f(x)的导数,判断导函数的单调性,利用函数在区间[2,e2+1]上不单调,列出不等式组,即可求实数a的取值范围;
(2)利用f(x)+x-1-k(x-2)>0求出k的不等式,利用函数的导数求解新函数在x>2的最小值,利用恒成立,即可求k的最大值.
(2)利用f(x)+x-1-k(x-2)>0求出k的不等式,利用函数的导数求解新函数在x>2的最小值,利用恒成立,即可求k的最大值.
解答:
解:(1)g'(x)=-a+1+ln(x-1)在(1,+∞)上递增 …(1分)
由已知,有
解得1<a<3
∴a的取值范围为(1,3).…(4分)
(2)由题知k<
对x>2恒成立.…(5分)
令u(x)=
则u'(x)=
令v(x)=-ln(x-1)+x-3v′(x)=1-
=
,
∵x>2∴v'(x)>0即v(x)在(2,+∞)上递增 …(8分)
又∵v(4)=-ln3+1<0,v(5)=-2ln2+2>0
∴?x0∈(4,5),使得v(x0)=0,即u'(x0)=0
∴u(x)在(4,x0)上递减,在(x0,5)上递增.…(10分)
∴[u(x)]min=u(x0)=
=
=x0-1∈(3,4)
k<[u(x)]min=x0-1
又∵k∈Z,∴k的最大值为3.…(12分)
由已知,有
|
∴a的取值范围为(1,3).…(4分)
(2)由题知k<
| (x-1)ln(x-1)+x-1 |
| x-2 |
令u(x)=
| (x-1)ln(x-1)+x-1 |
| x-2 |
| -ln(x-1)+x-3 |
| (x-2)2 |
令v(x)=-ln(x-1)+x-3v′(x)=1-
| 1 |
| x-1 |
| x-2 |
| x-1 |
∵x>2∴v'(x)>0即v(x)在(2,+∞)上递增 …(8分)
又∵v(4)=-ln3+1<0,v(5)=-2ln2+2>0
∴?x0∈(4,5),使得v(x0)=0,即u'(x0)=0
∴u(x)在(4,x0)上递减,在(x0,5)上递增.…(10分)
∴[u(x)]min=u(x0)=
| (x0-1)ln(x0-1)+(x0-1) |
| x0-2 |
| (x0-1)(x0-3)+(x0-1) |
| x0-2 |
k<[u(x)]min=x0-1
又∵k∈Z,∴k的最大值为3.…(12分)
点评:本题考查函数的导数的应用,函数的极值,构造法的应用,考查分析问题解决问题的能力,难度较大.

练习册系列答案
相关题目
已知方程|x-2|-kx+1=0有两个不相等的实根,则实数k的取值范围是( )
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,+∞) |
一植物园参观路径如图所示,若要全部参观并且路线不重复,则不同的参观路线种数共有( )
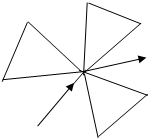

| A、6种 | B、8种 |
| C、36种 | D、48种 |