题目内容
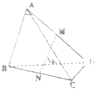 如图,在四面体ABCD中,若M、N分别是棱AD、BC的中点,AC=BD=6,MN=3
如图,在四面体ABCD中,若M、N分别是棱AD、BC的中点,AC=BD=6,MN=3| 2 |
考点:异面直线及其所成的角
专题:空间角
分析:取AB中点O,连结MO,NO,则NO∥AC,ON=
AC=3,MO=
BD=3,∠MNO是MN与AC所成的角(或所成角的补角),由此能求出MN与AC所成的角.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
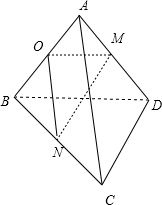 解:取AB中点O,连结MO,NO,
解:取AB中点O,连结MO,NO,
∵M、N分别是棱AD、BC的中点,AC=BD=6,MN=3
,
∴NO∥AC,ON=
AC=3,MO=
BD=3,
∴∠MNO是MN与AC所成的角(或所成角的补角),
cos∠MNO=
=
=0,
∴∠MNO=90°,
∴MN与AC所成的角为90°.
 解:取AB中点O,连结MO,NO,
解:取AB中点O,连结MO,NO,∵M、N分别是棱AD、BC的中点,AC=BD=6,MN=3
| 2 |
∴NO∥AC,ON=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MNO是MN与AC所成的角(或所成角的补角),
cos∠MNO=
| MO2+NO2-MN2 |
| 2MO•NO |
| 9+9-18 |
| 2×3×3 |
∴∠MNO=90°,
∴MN与AC所成的角为90°.
点评:本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.

练习册系列答案
相关题目
已知某离散型随机变量?分布列如下,则常数k的值为( )
| ? | 1 | 2 | 3 | … | n |
| P | k | 3k | 5k | … | (2n-1)k |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知
+
=1(m>0,n>0),则当m+n取得最小值时,椭圆
+
=1的离心率为( )
| 1 |
| m |
| 2 |
| n |
| x2 |
| m2 |
| y2 |
| n2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
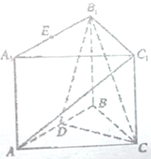 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.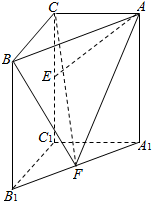 如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,E,F分别是CC1,A1B1的中点.