题目内容
9.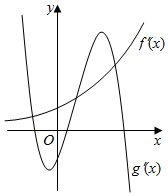 定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )
定义在R上的函数f(x)和g(x),其各自导函数f′(x)f和g′(x)的图象如图所示,则函数F(x)=f(x)-g(x)极值点的情况是( )| A. | 只有三个极大值点,无极小值点 | B. | 有两个极大值点,一个极小值点 | ||
| C. | 有一个极大值点,两个极小值点 | D. | 无极大值点,只有三个极小值点 |
分析 根据函数的单调性结合函数的图象判断函数的极值点的个数即可.
解答 解:F′(x)=f′(x)-g′(x),
由图象得f′(x)和g′(x)有3个交点,
从左到右分分别令为a,b,c,
故x∈(-∞,a)时,F′(x)<0,F(x)递减,
x∈(a,b)时,F′(x)>0,F(x)递增,
x∈(b,c)时,F′(x)<0,F(x)递减,
x∈(c,+∞)时,F′(x)>0,F(x)递增,
故函数F(x)有一个极大值点,两个极小值点,
故选:C.
点评 本题考查了函数的单调性、极值点问题,考查导数的应用以及数形结合思想,是一道中档题.

练习册系列答案
相关题目
20.已知函数f(x)=sin(ωx+φ)+1(ω>0,0≤φ≤$\frac{π}{2}$)的图象相邻两条对称轴之间的距离为π,且在x=$\frac{π}{3}$时取得最大值2,若f(α)=$\frac{8}{5}$,且$\frac{π}{3}$<α<$\frac{5π}{6}$,则sin(2α+$\frac{π}{3}$)的值为( )
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | -$\frac{24}{25}$ |
14.设函数f(x),g(x)在区间(0,5)内导数存在,且有以下数据:
则曲线f(x)在点(1,f(1))处的切线方程是y=3x-1;函数f(g(x))在x=2处的导数值是12.
| x | 1 | 2 | 3 | 4 |
| f(x) | 2 | 3 | 4 | 1 |
| f′(x) | 3 | 4 | 2 | 1 |
| g(x) | 3 | 1 | 4 | 2 |
| g′(x) | 2 | 4 | 1 | 3 |
1.若复数z1,z2在复平面内的对应点关于虚轴对称,且z1=1+i,则z2=( )
| A. | 1+i | B. | 1-i | C. | -1-i | D. | -1+i |
19.已知命题
p1:函数f(x)=ex-e-x在R上单调递增
p2:函数g(x)=ex+e-x在R上单调递减
则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2和q4:p1∧(¬p2)中,真命题是( )
p1:函数f(x)=ex-e-x在R上单调递增
p2:函数g(x)=ex+e-x在R上单调递减
则在命题q1:p1∨p2,q2:p1∧p2,q3:(¬p1)∨p2和q4:p1∧(¬p2)中,真命题是( )
| A. | q1,q3 | B. | q2,q3 | C. | q1,q4 | D. | q2,q4 |
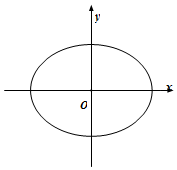 给定椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0).设t>0,过点T(0,t)斜率为k的 直线l与椭圆C交于M,N两点,O为坐标原点.
给定椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0).设t>0,过点T(0,t)斜率为k的 直线l与椭圆C交于M,N两点,O为坐标原点.