题目内容
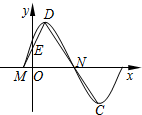 右图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
右图为函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<| π |
| 2 |
| MD |
| MN |
| π2 |
| 8 |
考点:函数y=Asin(ωx+φ)的图象变换,平面向量数量积的运算
专题:三角函数的图像与性质
分析:由已知点E(0,1)是线段MD的中点知A=2,根据
•
=
,求得ω=2,又由E(0,1)是线段MD的中点,分析可得D、M的坐标,进而可得φ的值,从而求得函数的解析式.
| MD |
| MN |
| π2 |
| 8 |
解答:
解:由已知点E(0,1)是线段MD的中点知A=2,根据
•
=
,
可得|
|•|
|•cos∠DMN=
•
2=
(
)2=
,求得ω=2.
∴函数f(x)=2sin(2x+φ),
又由E(0,1)是线段MD的中点,则D的纵坐标为2,且点M、D的横坐标互为相反数.
又由ω=2,则周期T=
=π.
设点D的横坐标为a,则点M的横坐标为-a,2a=
•T=
,∴a=
,
故M的坐标为(-
,0),D的坐标为(
,2).
根据五点法作图可得2•(-
)+φ=0,
可得φ=
,∴f(x)=2sin(2x+
),
故答案为:f(x)=2sin(2x+
).
| MD |
| MN |
| π2 |
| 8 |
可得|
| MD |
| MN |
| 1 |
| 2 |
| MN |
| 1 |
| 2 |
| π |
| ω |
| π2 |
| 8 |
∴函数f(x)=2sin(2x+φ),
又由E(0,1)是线段MD的中点,则D的纵坐标为2,且点M、D的横坐标互为相反数.
又由ω=2,则周期T=
| 2π |
| 2 |
设点D的横坐标为a,则点M的横坐标为-a,2a=
| 1 |
| 4 |
| π |
| 4 |
| π |
| 8 |
故M的坐标为(-
| π |
| 8 |
| π |
| 8 |
根据五点法作图可得2•(-
| π |
| 8 |
可得φ=
| π |
| 4 |
| π |
| 4 |
故答案为:f(x)=2sin(2x+
| π |
| 4 |
点评:本题主要考查利用y=Asin(ωx+∅)的图象特征,由函数y=Asin(ωx+∅)的部分图象求解析式,三角函数的恒等变换及化简求值,属于中档题.

练习册系列答案
相关题目
在△ABC中,AB=AC=3,∠BAC=30°,CD是边AB上的高,则
•
=( )
| CD |
| CB |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
阅读如图的程序框图,输出的值为( )


A、-
| ||
B、
| ||
| C、-1 | ||
D、-
|
 已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,|φ|<π)的一段图象如图所示. 一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的
一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的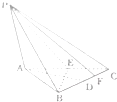 在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.
在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.