题目内容
以边长为1的正方形的一边所在所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于( )
| A、2π | B、π | C、2 | D、1 |
考点:旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的侧面积和表面积
专题:计算题,空间位置关系与距离
分析:边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,从而可求圆柱的侧面积.
解答:
解:边长为1的正方形,绕其一边所在直线旋转一周,得到的几何体为圆柱,
则所得几何体的侧面积为:1×2π×1=2π,
故选:A.
则所得几何体的侧面积为:1×2π×1=2π,
故选:A.
点评:本题是基础题,考查旋转体的侧面积的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数f(x)=
-log2x,在下列区间中,包含f(x)零点的区间是( )
| 6 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,4) |
| D、(4,+∞) |
已知i是虚数单位,i2=-1,则复数
在复平面上对应点的坐标是( )
| 5i |
| 2-i |
| A、(-1,2) |
| B、(1,-2) |
| C、(1,2) |
| D、(-1,-2) |
学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,则这一组学生最多有( )
| A、2人 | B、3人 | C、4人 | D、5人 |
正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A、
| ||
| B、16π | ||
| C、9π | ||
D、
|
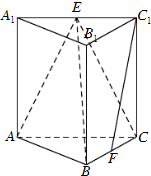 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.