题目内容
已知函数f(x)=x2-2x-3
(1)求函数的对称轴,顶点坐标和函数的单调区间;
(2)做出函数的图象;
(3)求函数的自变量在什么范围内取值时,函数值大于零.
(1)求函数的对称轴,顶点坐标和函数的单调区间;
(2)做出函数的图象;
(3)求函数的自变量在什么范围内取值时,函数值大于零.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据函数f(x)=x2-2x-3=(x-1)2-4,可得得函数的对称轴方程、顶点坐标、函数的单调增区间和减区间.
(2)做出函数的图象,如图所示.
(3)令f(x)=x2-2x-3=0,求得x=-1,或 x=3,数形结合可得自变量在什么范围内取值时,函数值大于零.
(2)做出函数的图象,如图所示.
(3)令f(x)=x2-2x-3=0,求得x=-1,或 x=3,数形结合可得自变量在什么范围内取值时,函数值大于零.
解答:
 解:(1)根据函数f(x)=x2-2x-3=(x-1)2-4,求得函数的对称轴方程为x=1,顶点坐标为(1,-4),
解:(1)根据函数f(x)=x2-2x-3=(x-1)2-4,求得函数的对称轴方程为x=1,顶点坐标为(1,-4),
函数的单调增区间为(1,+∞);减区间为(-∞,-1].
(2)作出函数的图象,如图所示:
(3)令f(x)=x2-2x-3=0,求得x=-1,或 x=3,数形结合可得,当x<-1,或 x>3 时,
函数值大于零.
 解:(1)根据函数f(x)=x2-2x-3=(x-1)2-4,求得函数的对称轴方程为x=1,顶点坐标为(1,-4),
解:(1)根据函数f(x)=x2-2x-3=(x-1)2-4,求得函数的对称轴方程为x=1,顶点坐标为(1,-4),函数的单调增区间为(1,+∞);减区间为(-∞,-1].
(2)作出函数的图象,如图所示:
(3)令f(x)=x2-2x-3=0,求得x=-1,或 x=3,数形结合可得,当x<-1,或 x>3 时,
函数值大于零.
点评:本题主要考查二次函数的图象性质,属于基础题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
在区间[-a,a](a>0)上,f(x)只是奇函数,g(x)只是偶函数,那么函数y=f(x)•g(x)( )
| A、只是奇函数 |
| B、只是偶函数 |
| C、既不是奇函数,也不是偶函数 |
| D、可能是奇函数,也可能是偶函数 |
正方体ABCD-A′B′C′D′中,异面直线AB′和A′D所成角为( )
| A、45° | B、60° |
| C、90° | D、60°或120° |
 已知直线l:2x-y+1=0和点A(-1,2)、B(0,3),试在l上找一点P,使得|PA|+|PB|的值最小,并求出这个最小值.
已知直线l:2x-y+1=0和点A(-1,2)、B(0,3),试在l上找一点P,使得|PA|+|PB|的值最小,并求出这个最小值. 如图,抛物线y=-x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x交抛物线y=-x2+bx+c对称轴右侧的抛物线于点P,连接PA、PC,设△AOP的面积为S1,△COP的面积为S2.
如图,抛物线y=-x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x交抛物线y=-x2+bx+c对称轴右侧的抛物线于点P,连接PA、PC,设△AOP的面积为S1,△COP的面积为S2.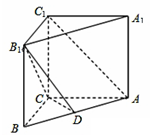 在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.
在直三棱柱ABC-A1B1C1中,已知AB=5,AC=4,BC=3,AA1=4,点D在棱AB上.