题目内容
18.经过双曲线x2-$\frac{{y}^{2}}{3}$=1的左焦点F1作倾斜角为$\frac{π}{6}$的弦AB.求:(1)线段AB的长;
(2)设F2为右焦点,求△F2AB的周长.
分析 (1)求出双曲线的焦点坐标,求出直线的斜率,利用点斜式求出直线方程;将直线的方程代入双曲线的方程,利用两点的距离公式求出|AB|.
(2)求出|BF2|,|AF2|,即可得到△F2AB的周长.
解答 解:(1)∵双曲线的左焦点为F1(-2,0),设A(x1,y1),B(x2,y2),
直线AB的方程可设为y=$\frac{\sqrt{3}}{3}$(x+2),代入方程x2-$\frac{{y}^{2}}{3}$=1得,8x2-4x-13=0,
∴x1+x2=$\frac{1}{2}$,x1x2=-$\frac{13}{8}$,
∴|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=3;
(2)|F1A|=$\sqrt{1+{k}^{2}}$|x1-(-2)|=$\frac{3\sqrt{3}-3}{2}$
由双曲线的定义得|BF2|=|BF1|-2=|AB|+|AF1|-2=1+$\frac{3\sqrt{3}-3}{2}$
|AF2|=|AF1|+2=2+$\frac{3\sqrt{3}-3}{2}$,
∴△F2AB的周长为3+3$\sqrt{3}$.
点评 本题考查直线与双曲线的位置关系,考查双曲线的定义,考查学生分析解决问题的能力,属于中档题.解决直线与圆锥曲线的弦长问题常将直线的方程与圆锥曲线方程联立,利用弦长公式.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
8.图中,能表示函数y=f(x)的图象的是( )
| A. |  | B. | 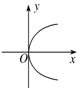 | C. |  | D. | 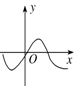 |
9.对任意实数a,b,c,d,定义符号$(\begin{array}{l}{a}&{b}\\{c}&{d}\end{array})$=$\left\{\begin{array}{l}{\sqrt{ad-bc}(ad≥bc)}\\{\frac{1}{2}\sqrt{bc-ad}(ad<bc)}\end{array}\right.$,已知函数f(x)=$(\begin{array}{l}{x}&{4}\\{1}&{x}\end{array})$,直线l:kx-y+3-2k=0,若直线l与函数f(x)的图象有两个公共点,则实数k的取值范围是( )
| A. | (-1,$\frac{2}{3}$)∪($\frac{3}{4}$,1) | B. | (-1,$\frac{17}{24}$) | C. | (-1,$\frac{17}{24}$)∪($\frac{3}{4}$,1) | D. | (-1,1) |
6.已知关于x的方程${({\frac{1}{2}})^x}-{x^{\frac{1}{3}}}=0$,那么在下列区间中含有方程的根的是( )
| A. | $(0,\frac{1}{3})$ | B. | $(\frac{1}{3},\frac{1}{2})$ | C. | $(\frac{1}{2},\frac{2}{3})$ | D. | $(\frac{2}{3},1)$ |