题目内容
6．已知关于x的方程${（{\frac{1}{2}}）^x}-{x^{\frac{1}{3}}}=0$，那么在下列区间中含有方程的根的是（ ）| A． | $（0，\frac{1}{3}）$ | B． | $（\frac{1}{3}，\frac{1}{2}）$ | C． | $（\frac{1}{2}，\frac{2}{3}）$ | D． | $（\frac{2}{3}，1）$ |
分析 根据函数的单调性以及函数零点的判断定理判断即可．
解答 解：令f（x）=${（\frac{1}{2}）}^{x}$-${x}^{\frac{1}{3}}$，显然f（x）在（0，+∞）递减，
而f（$\frac{1}{3}$）•f（$\frac{1}{2}$）＜0，
故f（x）在（$\frac{1}{3}$，$\frac{1}{2}$）有零点，
即关于x的方程${（{\frac{1}{2}}）^x}-{x^{\frac{1}{3}}}=0$，在区间（$\frac{1}{3}$，$\frac{1}{2}$）中含有方程的根，
故选：B．
点评 本题考查了函数的单调性以及函数零点的判定定理，是一道基础题．
练习册系列答案
考前必练系列答案
相关题目
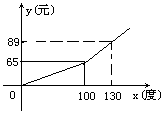西部大部分地区的电力紧缺，电力公司为鼓励市民节约用电，采取按月用电量分段收费办法，若某户居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解下列问题：