题目内容
9.对任意实数a,b,c,d,定义符号$(\begin{array}{l}{a}&{b}\\{c}&{d}\end{array})$=$\left\{\begin{array}{l}{\sqrt{ad-bc}(ad≥bc)}\\{\frac{1}{2}\sqrt{bc-ad}(ad<bc)}\end{array}\right.$,已知函数f(x)=$(\begin{array}{l}{x}&{4}\\{1}&{x}\end{array})$,直线l:kx-y+3-2k=0,若直线l与函数f(x)的图象有两个公共点,则实数k的取值范围是( )| A. | (-1,$\frac{2}{3}$)∪($\frac{3}{4}$,1) | B. | (-1,$\frac{17}{24}$) | C. | (-1,$\frac{17}{24}$)∪($\frac{3}{4}$,1) | D. | (-1,1) |
分析 函数f(x)=$(\begin{array}{l}{x}&{4}\\{1}&{x}\end{array})$=$\left\{\begin{array}{l}{\sqrt{{x}^{2}-4},x≥2或x≤-2}\\{\frac{1}{2}\sqrt{4-{x}^{2}},-2<x<2}\end{array}\right.$,直线l:kx-y+3-2k=0过定点A(2,3),
①当-2<x<2时,$\frac{{x}^{2}}{4}$+y2=1(椭圆上半部分),
②x≤-2或x≥2时,x2-y2=4(双曲线上半部分).如图所示.
画出图象,依据图象求解.
解答 解:函数f(x)=$(\begin{array}{l}{x}&{4}\\{1}&{x}\end{array})$=$\left\{\begin{array}{l}{\sqrt{{x}^{2}-4},x≥2或x≤-2}\\{\frac{1}{2}\sqrt{4-{x}^{2}},-2<x<2}\end{array}\right.$,
直线l:kx-y+3-2k=0过定点A(2,3),
①当-2<x<2时,$\frac{{x}^{2}}{4}$+y2=1(椭圆上半部分),
②x≤-2或x≥2时,x2-y2=4(双曲线上半部分).如图所示.
直线m与双曲线渐近线平行,直线l在直线m、n之间时满足条件,此时$\frac{3}{4}<k<1$,
直线e与双曲线渐近线平行,直线l在直线e、f之间时满足条件,此时
kx-y+3-2k=0代入椭圆方程可得:(1+4k2)x2+(24k-16k2)x+16k2-48k+32=0.
解得k=$\frac{2}{3}$
∵直线l:kx-y+3-2k=0与函数f(x)的图象有两个公共点,∴∴$-1<k<\frac{2}{3}$
综上所述,实数k的取值范围是(-1,$\frac{2}{3}$)∪($\frac{3}{4}$,1).
故选A
点评 本题考查了函数图象交点的个数问题,依据椭圆、双曲线的性质,结合图象是解本题的有效办法,属于中档题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | 若m∥α,α∥β则m∥β | B. | m∥α,m∥n则n∥α | C. | 若m∥α,n⊥α则m⊥n | D. | 若m∥α,n?α则m∥n |
| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
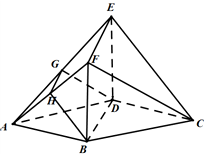 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=2,G和H分别是AE和AF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=2,G和H分别是AE和AF的中点.