题目内容
3.已知F是双曲线$C:{x^2}-\frac{y^2}{8}=1$的右焦点,P是C左支上一点,$A({0,6\sqrt{6}})$,当△APF周长最小时,点P的纵坐标为2$\sqrt{6}$.分析 设双曲线的左焦点为F',求出双曲线的a,b,c,运用双曲线的定义可得△PFA周长为|PA|+|PF|+|AF|=|PA|+|PF|+15,考虑P在左支上运动到与A,F'共线时,取得最小值,即可得到所求值.
解答 解:设双曲线的左焦点为F',
由双曲线$C:{x^2}-\frac{y^2}{8}=1$可得a=1,b=2$\sqrt{2}$,c=3,
即有F(3,0),F'(-3,0),
△PFA周长为|PA|+|PF|+|AF|=|PA|+|PF|+15,
由双曲线的定义可得|PF|-|PF'|=2a=2,
即有|PA|+|PF|=|PA|+|PF'|+2,
当P在左支上运动到A,P,F'共线时,|PA|+|PF'|取得最小值|AF'|,则有△APF周长取得最小值,
直线AF′的方程为$\frac{x}{-3}+\frac{y}{6\sqrt{6}}$=1,与双曲线方程联立,得到点P的纵坐标为2$\sqrt{6}$,
故答案为:2$\sqrt{6}$.
点评 本题考查三角形的周长的最小值,注意运用双曲线的定义和三点共线时取得最小值,考查运算能力,属于中档题.

练习册系列答案
相关题目
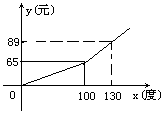 西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
西部大部分地区的电力紧缺,电力公司为鼓励市民节约用电,采取按月用电量分段收费办法,若某户居民每月应交电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题: