题目内容
已知矩阵M=(
),N=(
).
(Ⅰ)求使得MX=N成立的二阶矩阵X;
(Ⅱ)求矩阵X的特征值以及每个特征值所对应的一个特征向量.
|
|
(Ⅰ)求使得MX=N成立的二阶矩阵X;
(Ⅱ)求矩阵X的特征值以及每个特征值所对应的一个特征向量.
考点:特征值与特征向量的计算
专题:选作题,矩阵和变换
分析:(Ⅰ)求出M-1=
,利用X=M-1N,可求二阶矩阵X;
(Ⅱ)根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
|
(Ⅱ)根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量.
解答:
解:(Ⅰ)M=(
),|M|=-1,
∴M-1=
,
∴X=M-1N=
;
(Ⅱ)矩阵M的特征多项式为f(λ)=(λ+1)(λ+2),
令f(λ)=0,可求得特征值为λ1=-1,λ2=-2,
设λ1=-1对应的一个特征向量为α=
,
则由λ1α=Mα,得x+y=0,可令x=1,则y=-1,
∴矩阵M的一个特征值λ1=1对应的一个特征向量为
,
同理可得矩阵M的一个特征值λ2=-2对应的一个特征向量为
.
|
∴M-1=
|
∴X=M-1N=
|
(Ⅱ)矩阵M的特征多项式为f(λ)=(λ+1)(λ+2),
令f(λ)=0,可求得特征值为λ1=-1,λ2=-2,
设λ1=-1对应的一个特征向量为α=
|
则由λ1α=Mα,得x+y=0,可令x=1,则y=-1,
∴矩阵M的一个特征值λ1=1对应的一个特征向量为
|
同理可得矩阵M的一个特征值λ2=-2对应的一个特征向量为
|
点评:本小题主要考查矩阵与变换、矩阵的特征值与特征向量等基础知识,考查运算求解能力.

练习册系列答案
相关题目
7人站成一排,其中甲不排头,乙不排当中的不同排法种数为( )
| A、4000 | B、3720 |
| C、960 | D、1024 |
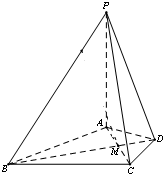 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°.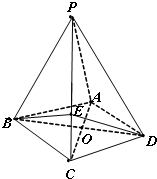 如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD.PA=AB=2,∠BAD=120°,E是PC上的一点,且BE与平面PAB所成角的正弦值为
如图,四棱锥P-ABCD中,底面ABCD为菱形,PA⊥底面ABCD.PA=AB=2,∠BAD=120°,E是PC上的一点,且BE与平面PAB所成角的正弦值为