下列函数中.在R上单调递增的是( )A．y=-xB．y=log3xC．$y={x^{\frac{1}{3}}}$D．y=x 题目和参考答案——青夏教育精英家教网—

题目内容

4．下列函数中，在R上单调递增的是（　　）

A．

y=-x

B．

y=log₃x

C．

$y={x^{\frac{1}{3}}}$

D．

y=（$\frac{1}{2}$）^x

分析分别根据函数的性质判断函数的单调性即可．

解答解：A．函数y=-x．在R上单调递J减，
B．函数y=log₃x在（0，+∞）上单调递增，
C．函数y=${x}^{\frac{1}{3}}$在R上单调递增，
D．函数y=（$\frac{1}{2}$）^x，在R上单调递减，
故选：C．

点评本题主要考查函数单调性的判断，要熟练掌握常见函数的单调性．

练习册系列答案

相关题目

14．不等式2^2x-1＜2的解集是（　　）

15．已知函数f（x）是定义在R上的奇函数，且当x＞0时，$f（x）={（\frac{1}{3}）^x}$
（1）求函数f（x）的解析式；
（2）直接写出单调区间，并计算f（log₃2+1）的值．

12．

如图，在平行六面体ABCD-A₁B₁C₁D₁中，M，N分别在面对角线AC，A₁C上且CM=2MA，A₁N=2ND．记向量$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，\overrightarrow{A{A_1}}=\overrightarrow c$，用$\overrightarrow a，\overrightarrow b，\overrightarrow c$表示$\overrightarrow{MN}$．

19．若平面α⊥平面β，且平面α内的一条直线a垂直于平面β内的一条直线b，则（　　）

	A．	直线a必垂直于平面β		B．	直线b必垂直于平面α
	C．	直线a不一定垂直于平面β		D．	过a的平面与过b的平面垂直

9．已知f（α）=$\frac{sin（2π-α）cos（π+α）cos（\frac{π}{2}-α）cos（\frac{11π}{2}-α）}{sin（3π-α）cos（\frac{π}{2}+α）sin（\frac{9π}{2}+α）}$+cos（2π-α）．
（1）化简f（α）；
（2）若f（α）=$\frac{\sqrt{10}}{5}$，求$\frac{1}{sinα}$+$\frac{1}{cosα}$的值．

16．

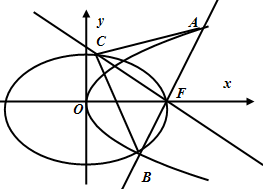如图，设椭圆C₁：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），长轴的右端点与抛物线C₂：y²=8x的焦点F重合，且椭圆C₁的离心率是$\frac{\sqrt{3}}{2}$．
（1）求椭圆C₁的标准方程；
（2）过F作直线l交抛物线C₂于A，B两点，过F且与直线l垂直的直线交椭圆C₁于另一点C，求△ABC面积的最小值，以及取到最小值时直线l的方程．

13．

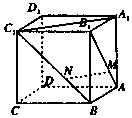正方体ABCD-A₁B₁C₁D₁中，点M、N分别在线段AB₁、BC₁上，且AM=BN．以下结论：①AA₁⊥MN；②A₁C₁∥MN；③MN∥平面A₁B₁C₁D₁；④MN与A₁C₁异面，⑤MN与 A₁C₁成30°．其中有可能成立的结论的个数为（　　）

14．已知a∈R，命题p：?x∈[-2，-1]，x²-a≥0，命题q：?x∈R，x²+2ax-（a-2）=0．
（1）若命题p为真命题，求实数a的取值范围；
（2）若命题“p∨q”为真命题，命题“p∧q”为假命题，求实数a的取值范围．

试题分类