题目内容
13．
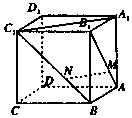正方体ABCD-A1B1C1D1中，点M、N分别在线段AB1、BC1上，且AM=BN．以下结论：①AA1⊥MN；②A1C1∥MN；③MN∥平面A1B1C1D1；④MN与A1C1异面，⑤MN与 A1C1成30°．其中有可能成立的结论的个数为（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
分析 ①作NE⊥BC，MF⊥AB，垂足分别为E，F，可得四边形MNEF是矩形，可得MN∥FE，利用AA1⊥面AC，可得结论成立；
由①知，MN∥面AC，面AC∥平面A1B1C1D1，故MN∥平面A1B1C1D1；
MN∥FE，FE与AC所在直线相交时，MN与A1C1异面，FE与AC平行时，则平行，故②④可能成立；
⑤EF与AC成30°时，MN与 A1C1成30°．
解答 解：①作NE⊥BC，MF⊥AB，垂足分别为E，F，
∵AM=BN，∴NE=MF，∴四边形MNEF是矩形，
∴MN∥FE，∵AA1⊥面AC，EF?面AC，∴AA1⊥EF，∴AA1⊥MN，故①正确；
由①知，MN∥面AC，面AC∥平面A1B1C1D1，∴MN∥平面A1B1C1D1，
故③正确；
MN∥FE，FE与AC所在直线相交时，MN与A1C1异面，FE与AC平行时，则平行，故②④可能成立；
⑤EF与AC成30°时，MN与 A1C1成30°．
故选A．
点评 本题考查线面平行、垂直，考查线面角的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
名校名卷单元同步训练测试题系列答案
相关题目
3．函数$y=\sqrt{1-{2^x}}$的定义域是（ ）
| A． | （-∞，0] | B． | [0，+∞） | C． | [1，+∞） | D． | （-∞，1] |
4．下列函数中，在R上单调递增的是（ ）
| A． | y=-x | B． | y=log3x | C． | $y={x^{\frac{1}{3}}}$ | D． | y=（$\frac{1}{2}$）x |
1．下列关于零向量的说法不正确的是（ ）
| A． | 零向量是没有方向的向量 | B． | 零向量的方向是任意的 | ||
| C． | 零向量与任一向量共线 | D． | 零向量只能与零向量相等 |
如图，四边形ABCD是平行四边形，平面AED⊥平面ABCD，EF∥AB，$BC=EF=\frac{1}{2}AB$，∠BAD=60°，G为BC的中点．
18．执行如图所示的程序框图，则输出的结果为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
据统计，我国每年交通事故死亡人数已经超过了10万人，我国汽车保有量不到全世界2%，但是交通事故死亡人数则占全球的20%，其中一个很重要的原因是国内很多驾驶员没有养成正确的驾驶习惯，没掌握事故发生前后正确的操作方法．某地交通管理部门从当地某驾校当期一班、二班学员中各随机抽取9名学员参加交通法规知识抽测，测试成绩绘制的茎叶图如下，其中有一个成绩模糊，用x表示．
某中学高三年级有400名学生参加月考，用简单随机抽样的方法抽取了一个容量为50的样本，得到数学成绩的频率分布直方图如图所示．