题目内容
7．设F1、F2分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，当a=2b时，点P在椭圆上，且PF1⊥PF2，|PF1|•|PF2|=2时，求椭圆方程．分析 利用已知条件列出方程，求出椭圆的a，b，即可得到椭圆方程．
解答 解：∵a=2b，a2=b2+c2，∴c2=3b2，
又∵PF1⊥PF2，∴|PF1|2+|PF2|2=（2c）2=12b2，
由椭圆定义可知|PF1|+|PF2|=2a=4b，
（|PF1|+|PF2|）2=12b2+4=16b2，
从而得b2=1，a2=4，
∴椭圆方程为：$\frac{{x}^{2}}{4}+{y}^{2}=1$．
点评 本题考查椭圆方程的求法，椭圆的简单性质的应用，考查计算能力．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
3．已知函数f（x）是定义在（-8，8）上的偶函数，f（x）在[0，8）上是单调函数，且f（-3）＜f（2）则下列不等式成立的是（ ）
| A． | f（-1）＜f（1）＜f（3） | B． | f（2）＜f（3）＜f（-4） | C． | f（-2）＜f（0）＜f（1） | D． | f（5）＜f（-3）＜f（-1） |
12．已知锐角α终边上一点A的坐标为（2sin3，-2cos3），则角α的弧度数为（ ）
| A． | 3 | B． | π-3 | C． | 3-$\frac{π}{2}$ | D． | $\frac{π}{2}$-3 |
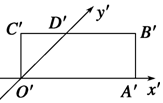如图，矩形O′A′B′C′是水平放置的一个平面图形的斜二测画法画出的直观图，其中O′A′=6cm，C′D′=2cm，则原图形是（ ）