题目内容
函数f(x)=ln(x+m)+n的图象在点(1,f(1))处的切线方程是y=x-1,函数g(x)=ax2+bx(a,b∈R,a≠0)在x=2处取极值-2.
(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)若函数y=f(x+1)-g′(x)(其中g′(x)是g(x)的导函数)在区间(t,t+
)(t>-1)上没有单调性,求实数t的取值范围.
(Ⅰ)求函数f(x),g(x)的解析式;
(Ⅱ)若函数y=f(x+1)-g′(x)(其中g′(x)是g(x)的导函数)在区间(t,t+
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)由已知条件结合导数性质得函数f(x)=lnx,g(x)=
x2-2x.
(Ⅱ)y=f(x+1)-g'(x)=ln(x+1)-x+2(x>-1),从而y′=
-1=
,由此利用导数性质能求出实数t的取值范围.
| 1 |
| 2 |
(Ⅱ)y=f(x+1)-g'(x)=ln(x+1)-x+2(x>-1),从而y′=
| 1 |
| x+1 |
| -x |
| x+1 |
解答:
(本小题满分13分)
解:(Ⅰ)f′(x)=
,则f′(1)=
=1,
∴m=0,又f(1)=0,∴n=0,故函数f(x)=lnx
又g'(x)=2ax+b,
则
,
解得
∴g(x)=
x2-2x.
(Ⅱ)y=f(x+1)-g'(x)=ln(x+1)-x+2(x>-1),
∴y′=
-1=
,
由y'>0,解得-1<x<0;由y'<0,解得x>0.
故该函数在区间(-1,0)上为增函数,
在区间(0,+∞)上为减函数.
又y=f(x+1)-g'(x)在区间(t,t+
)上没有单调性,
则
,解得-
<t<0
故实数t的取值范围是(-
,0).
解:(Ⅰ)f′(x)=
| 1 |
| x+m |
| 1 |
| 1+m |
∴m=0,又f(1)=0,∴n=0,故函数f(x)=lnx
又g'(x)=2ax+b,
则
|
解得
|
| 1 |
| 2 |
(Ⅱ)y=f(x+1)-g'(x)=ln(x+1)-x+2(x>-1),
∴y′=
| 1 |
| x+1 |
| -x |
| x+1 |
由y'>0,解得-1<x<0;由y'<0,解得x>0.
故该函数在区间(-1,0)上为增函数,
在区间(0,+∞)上为减函数.
又y=f(x+1)-g'(x)在区间(t,t+
| 1 |
| 2 |
则
|
| 1 |
| 2 |
故实数t的取值范围是(-
| 1 |
| 2 |
点评:本题考查函数的解析式的求法,考查实数的取值范围的求法,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
已知集合p={x|(x-1)(x-3)≤0},Q={x||x|<2},则p∪Q等于( )
| A、[1,2) |
| B、[1,3] |
| C、(-2,3] |
| D、(-2,2) |
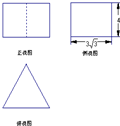 已知一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,大致画出它的直观图,并求出它的表面积和体积.
已知一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图所示,大致画出它的直观图,并求出它的表面积和体积.