题目内容
 如图所示,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3cm,周期为3s,且物体向右运动到A点(距平衡位置最远处)开始计时.
如图所示,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3cm,周期为3s,且物体向右运动到A点(距平衡位置最远处)开始计时.(1)求物体离开平衡位置的位移x(cm)和时间t(s)之间的函数关系式;
(2)求该物体在t=5s时的位置.
考点:函数解析式的求解及常用方法
专题:应用题
分析:第(1)问要分析出这是一个三角函数模型,用待定系数法求解,根据题意设出函数的形式,然后利用条件求解系数;第(2)问代入第(1)问的解析式即可求出.
解答:
解:(1)设位移x(cm)和时间t(s)之间的函数关系式为x=3sin(ωt+φ)(ω>0,0≤φ<2π),
则由T=
=3,得ω=
.
当t=0时,有x=3sin φ=3,∴sin φ=1.又0≤φ<2π,故可得φ=
.
从而所求的函数关系式是x=3sin(
t+
),即为x=3cos
t.
(2)令t=5,得x=3cos
=-1.5,
故该物体在t=5 s时的位置是在O点左侧且距O点1.5 cm 处.

则由T=
| 2π |
| ω |
| 2π |
| 3 |
当t=0时,有x=3sin φ=3,∴sin φ=1.又0≤φ<2π,故可得φ=
| π |
| 2 |
从而所求的函数关系式是x=3sin(
| 2π |
| 3 |
| π |
| 2 |
| 2π |
| 3 |
(2)令t=5,得x=3cos
| 10π |
| 3 |
故该物体在t=5 s时的位置是在O点左侧且距O点1.5 cm 处.
点评:本题通过实际问题考查了三解函数求解析式及代入求值,在求φ时要注意φ的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在(-π,4π)内与-
终边相同的角有( )个.
| 5π |
| 4 |
| A、0 | B、1 | C、2 | D、3 |
将函数y=sin(x+
)图象上各点的横坐标缩短到原来的
倍(纵坐标不变),再向右平移
个单位,那么所得图象的一条对称轴方程为( )
| π |
| 6 |
| 1 |
| 2 |
| π |
| 3 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=
|
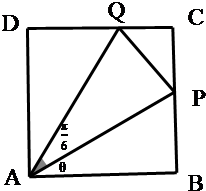 如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=
如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=