Question

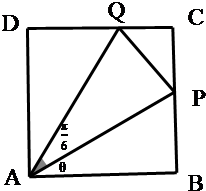如图，某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质，其形状为三角形APQ，其中P位于边CB上，Q位于边CD上．已知AB=20米，∠PAQ=

π

6

，设∠PAB=θ，记f（θ）=

正方形ABCD面积

APAQ面积

，当f（θ）越大，则污水净化效果越好．
（1）求f（θ）关于的函数解析式，并求定义域；
（2）求f（θ）最大值，并指出等号成立条件？

Answer 1

考点：三角函数中的恒等变换应用

专题：综合题,解三角形

分析：（1）首先求出θ的范围，然后分别表示出AP，AQ，和三角形APQ的面积，进而获得f（θ）的解析式．
（2）对函数解析式利用两角和公式进行化简整理，利用θ的范围和三角函数的性质求得函数的最大值．

解答： 解：（1）∵0＜θ＜

π

4

，0＜

π

3

-θ＜

π

4

，
∴

π

12

＜θ＜

π

4

，
如图AP=

20

cosθ

，AQ=

20

cos( π 3 -θ)

，S△APQ=

1

2

AP•AQsin

π

6

=

100

cosθ•cos( π 3 -θ)

，
∴f(θ)=

400

100 cosθ•cos( π 3 -θ)

=4cosθ•cos(

π

3

-θ)，θ∈[

π

12

，

π

4

]
（2）f(θ)=2cos2θ+2

3

sinθcosθ=cos2θ+

3

sin2θ+1=2sin(2θ+

π

6

)+1，
∵θ∈[

π

12

，

π

4

]
∴

π

3

＜2θ+

π

6

＜

2

3

π，
∴当2θ+

π

6

=

π

2

时，即θ=

π

6

时，f（θ）_max=3，
答：当θ=

π

6

时，f（θ）的最大值为3．

点评：本题主要考查了三角函数恒等变换的应用．考查了学生运用三角函数基础知识解决实际问题的能力．