题目内容
6．已知A={（x，y）|x2+y2=1}，B={（x，y）|x+y=1}，则A∩B的元素个数是2．分析 构成方程组，即可求出交点，即可做出判断．
解答 解：由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=1}\\{x+y=1}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$，
∴A={（x，y）|x2+y2=1}，B={（x，y）|x+y=1}，则A∩B的元素个数是2个，
故答案为：2
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
高中必刷题系列答案
相关题目
16．在△ABC中，内角A，B，C所对的边分别是a，b，c，已知a=7，c=5，则$\frac{sinA}{sinC}$的值是（ ）
| A． | $\frac{7}{5}$ | B． | $\frac{5}{7}$ | C． | $±\frac{7}{12}$ | D． | $\frac{5}{12}$ |
1．曲线f（x）=$\frac{2}{{{x^2}-1}}$、直线x=2、x=3以及x轴所围成的封闭图形的面积是（ ）
| A． | ln2 | B． | ln3 | C． | 2ln2 | D． | $ln\frac{3}{2}$ |
11．如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的体积为（ ）
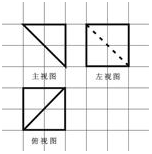
| A． | $\frac{8}{3}$ | B． | $\frac{4}{3}$ | C． | 4$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
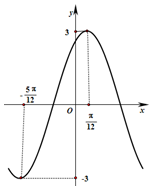函数y=Asin（ω•x+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则此函数的解析式为y=3sin（2x+$\frac{π}{3}$）．