题目内容
设实数x,y满足
,则μ=
的取值范围是( )
|
| y |
| x |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[2,
|
考点:简单线性规划
专题:计算题,不等式的解法及应用,直线与圆
分析:根据不等式组画出可行域,得到如图所示的△ABC及其内部的区域.设P(x,y)为区域内一点,根据斜率计算公式可得μ=
表示直线OP的斜率,运动点P得到PQ斜率的最大、最小值,即可得到μ=
的取值范围.
| y |
| x |
| y |
| x |
解答:
解:作出不等式组表示的平面区域,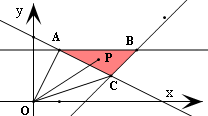 得到如图所示的△ABC及其内部的区域
得到如图所示的△ABC及其内部的区域
其中A(1,2),B(4,2),C(3,1)
设P(x,y)为区域内的动点,可得μ=
表示直线OP的斜率,
其中P(x,y)在区域内运动,O是坐标原点.
运动点P,可得当P与A点重合时,μ=2达到最大值;
当P与C点重合时,μ=
达到最小值.
综上所述,μ=
的取值范围是[
,2]
故选:A
 得到如图所示的△ABC及其内部的区域
得到如图所示的△ABC及其内部的区域其中A(1,2),B(4,2),C(3,1)
设P(x,y)为区域内的动点,可得μ=
| y |
| x |
其中P(x,y)在区域内运动,O是坐标原点.
运动点P,可得当P与A点重合时,μ=2达到最大值;
当P与C点重合时,μ=
| 1 |
| 3 |
综上所述,μ=
| y |
| x |
| 1 |
| 3 |
故选:A
点评:本题给出二元一次不等式组,求μ=
的取值范围.着重考查了直线的斜率公式、二元一次不等式组表示的平面区域和简单的线性规划等知识,属于中档题.
| y |
| x |

练习册系列答案
相关题目
已知函数f(x)=3x2-(k-2)x-8在[5,10]上具有单调性,则实数k的取值范围是( )
| A、[32,62] |
| B、(-∞,32]∪[62,+∞) |
| C、(32,62) |
| D、(-∞,32)∪(62,+∞) |
已知函数f(x)的图象是连续不断的,有如下x,f(x)对应值表:
其中a<c<0<b,则函数f(x)在区间[1,6]上零点至少有( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 10 | 13 | c | 7 | a | b |
| A、2个 | B、3个 | C、4个 | D、5个 |
实数x,y满足
,则z=x-3y的最小值为( )
|
| A、4 | B、-2 | C、-8 | D、-10 |
若点(a,-1)在函数y=log
x的图象上,则tan
的值为( )
| 1 |
| 2 |
| aπ |
| 6 |
| A、0 | ||||
B、
| ||||
| C、1 | ||||
D、
|
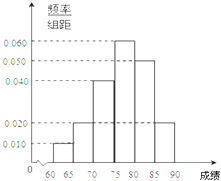 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.