题目内容
已知函数f(x)=3x2-(k-2)x-8在[5,10]上具有单调性,则实数k的取值范围是( )
| A、[32,62] |
| B、(-∞,32]∪[62,+∞) |
| C、(32,62) |
| D、(-∞,32)∪(62,+∞) |
考点:二次函数的性质
专题:函数的性质及应用
分析:根据二次函数单调性和对称轴之间的关系,建立条件关系即可.
解答:
解:∵函数f(x)=3x2-(k-2)x-8的对称轴为x=-
=
,
∴要使函数f(x)在[5,10]上具有单调性,
则
≤5或
≥10,
即k≤32或k≥62,
∴实数k的取值范围是(-∞,32]∪[62,+∞).
故选:B.
| -(k-2) |
| 2×3 |
| k-2 |
| 6 |
∴要使函数f(x)在[5,10]上具有单调性,
则
| k-2 |
| 6 |
| k-2 |
| 6 |
即k≤32或k≥62,
∴实数k的取值范围是(-∞,32]∪[62,+∞).
故选:B.
点评:本题主要考查二次函数的图象和性质,根据二次函数单调性和对称轴之间的关系是解决本题的关键.

练习册系列答案
相关题目
函数f(x)=
-(
)x的零点个数为( )
| x |
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、3 |
若实数x,y满足条件
则z=3x-4y的最大值是( )
|
| A、-13 | B、-3 | C、-1 | D、1 |
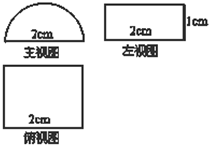 已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的表面积是( )(单位cm)
已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的表面积是( )(单位cm)| A、6+2π | B、4+2π |
| C、6+3π | D、4+3π |
设实数x,y满足
,则μ=
的取值范围是( )
|
| y |
| x |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[2,
|
