题目内容
给出下列四个结论:
①若A、B、C、D是平面内四点,则必有
+
=
+
;
②对于命题p:?x∈R,使得x2+x+1<0,则?p:?x∈R,均有x2+x+1>0;
③若函数f(x)=
,则f(
-1)的值为0;
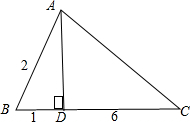
④△ABC中,∠ABC=60°,AB=2,BC=6,BC边上任取一点D,使△ABD为钝角三角形的概率为
.
其中正确结论的序号是 .(填上所有正确结论的序号)
①若A、B、C、D是平面内四点,则必有
| AC |
| BD |
| BC |
| AD |
②对于命题p:?x∈R,使得x2+x+1<0,则?p:?x∈R,均有x2+x+1>0;
③若函数f(x)=
|
| 1 |
| e |
④△ABC中,∠ABC=60°,AB=2,BC=6,BC边上任取一点D,使△ABD为钝角三角形的概率为
| 1 |
| 6 |
其中正确结论的序号是
考点:命题的真假判断与应用
专题:综合题
分析:①中,平面向量的运算得出
+
=
+
,判定①正确;
②中,写出命题p的否定?p,判定②错误;
③中,由解析式求出f(
-1)的值,判定③正确;
④中,根据题意,讨论△ABD为钝角三角形的情况,求出对应的概率,得出结论.
| AC |
| BD |
| BC |
| AD |
②中,写出命题p的否定?p,判定②错误;
③中,由解析式求出f(
| 1 |
| e |
④中,根据题意,讨论△ABD为钝角三角形的情况,求出对应的概率,得出结论.
解答:
 解:对于①,∵
解:对于①,∵
+
=(
+
)+
=
+
,∴①正确;
对于②,命题p:?x∈R,使得x2+x+1<0,的否定是?p:?x∈R,均有x2+x+1≥0,∴②错误;
对于③,∵
-1<0,∴f(
-1)=f(
)+1=ln
+1=-1+1=0,∴③正确;
对于④,第一种∠ADB为钝角,这种情况的边界是∠ADB=90°的时候,此时BD=1;∴这种情况下,必有0<BD<1;
第二种∠BAD为钝角,这种情况的边界是∠BAD=90°的时候,此时BD=4,
∴这种情况下,必有4<BD<6;
综合两种情况,若△ABD为钝角三角形,则0<BD<1或4<OC<6;
∴概率P=
+
=
,∴④错误;
综上,以上正确的结论是①③.
故答案为:①③.
 解:对于①,∵
解:对于①,∵| AC |
| BD |
| AB |
| BC |
| BD |
| BC |
| AD |
对于②,命题p:?x∈R,使得x2+x+1<0,的否定是?p:?x∈R,均有x2+x+1≥0,∴②错误;
对于③,∵
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
| 1 |
| e |
对于④,第一种∠ADB为钝角,这种情况的边界是∠ADB=90°的时候,此时BD=1;∴这种情况下,必有0<BD<1;
第二种∠BAD为钝角,这种情况的边界是∠BAD=90°的时候,此时BD=4,
∴这种情况下,必有4<BD<6;
综合两种情况,若△ABD为钝角三角形,则0<BD<1或4<OC<6;
∴概率P=
| 1 |
| 6 |
| 2 |
| 6 |
| 1 |
| 2 |
综上,以上正确的结论是①③.
故答案为:①③.
点评:本题通过命题真假的判定,考查了平面向量的加法运算,命题的否定,分段函数的解析式应用以及几何概型的计算等知识,解题时应对每一个命题认真分析,以便得出正确的结论,是基础题目.

练习册系列答案
相关题目
将函数y=cos(
-2x)的图象向右平移
个单位后所得的图象的一个对称轴是( )
| π |
| 6 |
| π |
| 12 |
A、x=
| ||
B、x=
| ||
C、x=
| ||
D、x=
|
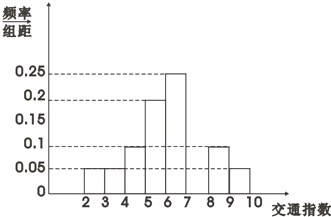 交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.
交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.