题目内容
 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AD垂直于AB和DC,侧棱SA⊥底面ABCD,且SA=2,AD=DC=1,点E在SD上,且AE⊥SD.(1)证明:AE⊥平面SDC;
(2)求三棱锥B-ECD的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)证明AE⊥平面SDC,只需证明AE⊥CD,利用证明CD⊥侧面SAD可得;
(2)证明CD⊥平面ASD,AB∥平面SCD,可得点B到平面SCD的距离等于点A到平面SCD的距离AE,即可求三棱锥B-ECD的体积.
(2)证明CD⊥平面ASD,AB∥平面SCD,可得点B到平面SCD的距离等于点A到平面SCD的距离AE,即可求三棱锥B-ECD的体积.
解答:
(1)证明:∵侧棱SA⊥底面ABCD,CD?底面ABCD,
∴SA⊥CD.….(1分)
∵底面ABCD直角梯形,AD垂直于AB和DC,
∴AD⊥CD,
又AD∩SA=A,
∴CD⊥侧面SAD,….(3分)
∵AE?侧面SAD
∴AE⊥CD,
∵AE⊥SD,CD∩SD=D,
∴AE⊥平面SDC….(5分)
(Ⅱ)解:∵CD⊥AD,CD⊥AE,AD∩AE=A,
∴CD⊥平面ASD,
∴CD⊥SD,
∴S△EDC=
ED•DC …(7分)
在Rt△ASD中,SA=2,AD=1,AE⊥SD,
∴ED=
,AE=
∴S△EDC=1,…(9分)
又∵AB∥CD,CD?平面SCD,AB?平面SCD,
∴AB∥平面SCD,
∴点B到平面SCD的距离等于点A到平面SCD的距离AE …(11分)
∴VB-ECD=
•S△EDC•AE=
…(12分)
∴SA⊥CD.….(1分)
∵底面ABCD直角梯形,AD垂直于AB和DC,
∴AD⊥CD,
又AD∩SA=A,
∴CD⊥侧面SAD,….(3分)
∵AE?侧面SAD
∴AE⊥CD,
∵AE⊥SD,CD∩SD=D,
∴AE⊥平面SDC….(5分)
(Ⅱ)解:∵CD⊥AD,CD⊥AE,AD∩AE=A,
∴CD⊥平面ASD,
∴CD⊥SD,
∴S△EDC=
| 1 |
| 2 |
在Rt△ASD中,SA=2,AD=1,AE⊥SD,
∴ED=
| 1 | ||
|
| 2 | ||
|
∴S△EDC=1,…(9分)
又∵AB∥CD,CD?平面SCD,AB?平面SCD,
∴AB∥平面SCD,
∴点B到平面SCD的距离等于点A到平面SCD的距离AE …(11分)
∴VB-ECD=
| 1 |
| 3 |
2
| ||
| 15 |
点评:本题考查线面垂直的判断与性质,考查三棱锥体积的计算,考查学生分析解决问题的能力.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
已知i为虚数单位,则i(1+i)2=( )
| A、2i | B、-2i | C、2 | D、-2 |
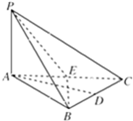 如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点.
如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点.
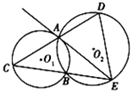 已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.
已知⊙O1和⊙O2相交于A,B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.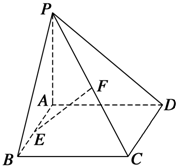 如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.求证:
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.求证: 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥底面ABCD,AB=2
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形,AA1⊥底面ABCD,AB=2