题目内容
(Ⅰ)求证:
+
<2
(Ⅱ)已知a>0,b>0且a+b>2,求证:
,
中至少有一个小于2.
| 3 |
| 7 |
| 5 |
(Ⅱ)已知a>0,b>0且a+b>2,求证:
| 1+b |
| a |
| 1+a |
| b |
考点:不等式的证明
专题:不等式
分析:(Ⅰ)利用了分析法,和两边平方法,
(Ⅱ)利用了反证法,假设:
,
都不小于2,则
≥2,
≥2,推得即a+b≤2,这与已知a+b>2矛盾,故假设不成立,从而原结论成立.
(Ⅱ)利用了反证法,假设:
| 1+b |
| a |
| 1+a |
| b |
| 1+b |
| a |
| 1+a |
| b |
解答:
(Ⅰ)证明:因为
+
和2
都是正数,所以为了证明
+
<2
,
只要证 (
+
)2<(2
)2
只需证:10+2
<20,
即证:2
<10,
即证:
<5,
即证:21<25,
因为21<25显然成立,所以原不等式成立.
(Ⅱ)证明:假设:
,
都不小于2,则
≥2,
≥2,
∵a>0,b>0,
∴1+b≥2a,1+a≥2b,
∴1+b+1+a≥2(a+b)
即 a+b≤2
这与已知a+b>2矛盾,故假设不成立,从而原结论成立.
| 3 |
| 7 |
| 5 |
| 3 |
| 7 |
| 5 |
只要证 (
| 3 |
| 7 |
| 5 |
只需证:10+2
| 21 |
即证:2
| 21 |
即证:
| 21 |
即证:21<25,
因为21<25显然成立,所以原不等式成立.
(Ⅱ)证明:假设:
| 1+b |
| a |
| 1+a |
| b |
| 1+b |
| a |
| 1+a |
| b |
∵a>0,b>0,
∴1+b≥2a,1+a≥2b,
∴1+b+1+a≥2(a+b)
即 a+b≤2
这与已知a+b>2矛盾,故假设不成立,从而原结论成立.
点评:本题主要考查了推理论证的两种方法分析法和反证法,属于中档题.

练习册系列答案
相关题目
已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则A∪B=( )
| A、{2} |
| B、{2,3,4} |
| C、{1,2,3,4} |
| D、{0,2,3,4} |
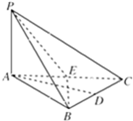 如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点.
如图,三棱锥P-ABC中,PA⊥底面ABC,△ABC为正三角形,D、E分别是BC、CA的中点.
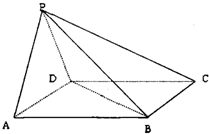 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且AD=