题目内容
已知函数f(x)=
,若关于x的方程:[f(x)]3+b[f(x)]2+c[f(x)]+d=0有且仅有3个不同的实根x1,x2,x3,则x12+x22+x32的值是 .
|
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:题中原方程f2(x)+af(x)+b=3有且只有3个不同实数解,即要求对应于方程:f(x)=某个常数,有3个不同实数解,故先根据题意作出f(x)的简图,由图可知,只有当f(x)=1时,它有三个根.故关于x的方程f2(x)+af(x)+b=3有且只有3个不同实数解,即解分别是1,2,3.从而问题解决.
解答:
解:∵函数f(x)=
,
∴f(2)=1,f(x)=1,x=0,或x=4,即f(0)=f(4)=1,
作出f(x)的简图:
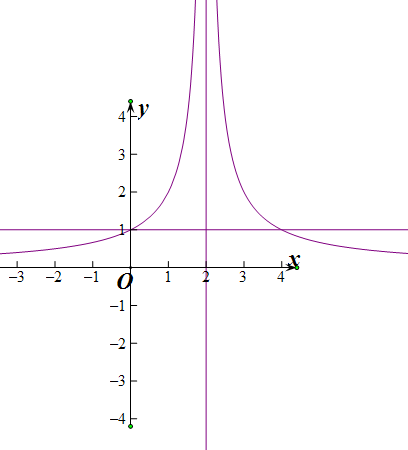
由图可知,只有当f(x)=1时,它有三个根.
故关于x的方程f2(x)+af(x)+b=3有且只有3个不同实数解,
即解分别是0,2,4.
故x12+x22+x32=0+4+16=20,
故答案为:20,
|
∴f(2)=1,f(x)=1,x=0,或x=4,即f(0)=f(4)=1,
作出f(x)的简图:

由图可知,只有当f(x)=1时,它有三个根.
故关于x的方程f2(x)+af(x)+b=3有且只有3个不同实数解,
即解分别是0,2,4.
故x12+x22+x32=0+4+16=20,
故答案为:20,
点评:本小题主要考查函数的零点与方程根的关系、函数的图象等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
已知命题p:2x2-x-1<0,那么p成立的一个必要不充分条件是( )
| A、0<x<1 | ||
| B、-1<x<1 | ||
C、-
| ||
D、-
|
原点和点(1,1)在直线x+y=a两侧,则a的取值范围是( )
| A、0<a<2 |
| B、a<0或a>2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
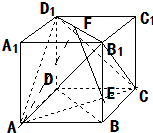 如图所示,在正方形ABCD-A1B1C1D1中,E、F分别是BB1、D1B1的中点.求证:EF⊥平面B1AC.
如图所示,在正方形ABCD-A1B1C1D1中,E、F分别是BB1、D1B1的中点.求证:EF⊥平面B1AC.