题目内容
过双曲线的一个焦点F2作实轴的垂线交双曲线于P、Q两点，F1是双曲线的另一个焦点，且∠PF1Q=60°，求双曲线的离心率．
考点：双曲线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据题意，△PQF1是等腰直角三角形，且被F1F2分成两个全等的直角三角形．由此结合双曲线的定义，可解出a、c关系，即可得到该双曲线的离心率．
解答：
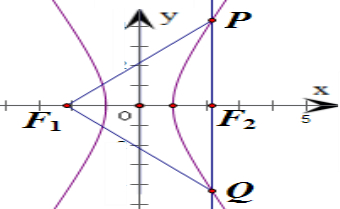解：根据双曲线的对称性得|PF1|=|QF1|
∵△PQF1中，∠PF1Q=60°，
∴△PQF1是一个角为30°的直角三角形，因此，Rt△PF1F2中，|F1F2|=
|PF2|=2c，|PF2|=
，
|F1F2|=2c，∴2c=
=
，
由此可得，
e2-2e-
=0，
双曲线的离心率e=
．
解：根据双曲线的对称性得|PF1|=|QF1|∵△PQF1中，∠PF1Q=60°，
∴△PQF1是一个角为30°的直角三角形，因此，Rt△PF1F2中，|F1F2|=
| 3 |
| b2 |
| a |
|F1F2|=2c，∴2c=
| 3 |
| b2 |
| a |
| ||
| a |
由此可得，
| 3 |
| 3 |
双曲线的离心率e=
| 3 |
点评：本题给出双曲线方程，在已知过右焦点的通径和左焦点构成等边三角形的情况下求双曲线的离心率，着重考查了双曲线的标准方程和简单几何性质等知识，属于中档题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知m，n为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（ ）
| A、m?α，n?α，m∥β，n∥β⇒α∥β |
| B、α∥β，m?α，n∥β⇒m∥n |
| C、m⊥α，m⊥n⇒n∥α |
| D、m∥n，n⊥α⇒m⊥α |