题目内容
 已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.
已知平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,GB=GD,求证:GO⊥平面ABCD.考点:直线与平面垂直的判定
专题:证明题,空间位置关系与距离
分析:证明GO⊥AC,GO⊥BD,利用线面垂直的判定定理,即可证明GO⊥平面ABCD.
解答:
证明:∵平行四边形ABCD的对角线相交于点O,G是平行四边形ABCD所在平面外一点,且GA=GC,
∴GO⊥AC.
又GB=GD,得GO⊥BD,
∵AC∩BD=O,
∴GO⊥平面ABCD.
∴GO⊥AC.
又GB=GD,得GO⊥BD,
∵AC∩BD=O,
∴GO⊥平面ABCD.
点评:本题考查线面垂直的判定定理,考查学生分析解决问题的能力,难度中等.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
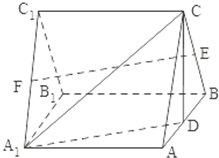 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.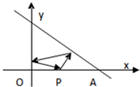 如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射到P点.求(1)光线所经过的路程是多少;(2)直线AB关于直线2x-y-2=0的对称直线.
如图,已知A(4,0)、B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射到P点.求(1)光线所经过的路程是多少;(2)直线AB关于直线2x-y-2=0的对称直线.