题目内容
2.已知△ABC三内角A,B,C所对边分别为a,b,c.(Ⅰ)若a,b,c成等比数列,求角B的最大值;
(Ⅱ)若a2,b2,c2成等差数列,求角B的最大值.
分析 (Ⅰ)根据题意得出,b2=ac,利用余弦定理,基本不等式求解即可,
(Ⅱ)根据题意得出,b2=$\frac{{a}^{2}+{c}^{2}}{2}$,利用余弦定理,基本不等式求解即可,
解答 解(Ⅰ)由已知得b2=ac,
由余弦定理$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{{a^2}+{c^2}-ac}}{2ac}=\frac{1}{2}(\frac{a}{c}+\frac{c}{a})-\frac{1}{2}≥\frac{1}{2}×2-\frac{1}{2}=\frac{1}{2}$,
当a=c时,cosB取得最小值,即角B取得最大值$\frac{π}{3}$;
(Ⅱ)由已知得${b^2}=\frac{{{a^2}+{c^2}}}{2}$,
由余弦定理$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{{{a^2}+{c^2}}}{4ac}=\frac{1}{4}(\frac{a}{c}+\frac{c}{a})≥\frac{1}{4}×2=\frac{1}{2}$,
当a=c时,cosB取得最小值,即角B取得最大值$\frac{π}{3}$.
点评 本题考查解斜三角形,运用余弦定理,基本不等式求解,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
12.设数列{an}的前n项和为Sn,a4=7且4Sn=n(an+an+1),则a5等于( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
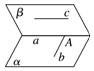 如图,已知平面α∩平面β=直线a,直线b?α,直线c?β,b∩a=A,c∥a.求证:b与c是异面直线.
如图,已知平面α∩平面β=直线a,直线b?α,直线c?β,b∩a=A,c∥a.求证:b与c是异面直线.