题目内容
12.i是虚数单位,若实数x,y满足(1+i)x+(1-i)y=2,z=$\frac{x+i}{y-i}$,则复数z的虚部等于( )| A. | 1 | B. | 0 | C. | -i | D. | i |
分析 利用复数相等、复数的运算法则、虚部的定义即可得出.
解答 解:实数x,y满足(1+i)x+(1-i)y=2,
∴x+y-2+(x-y)i=0,
∴x+y-2=x-y=0,解得x=y=1.
∴z=$\frac{x+i}{y-i}$=$\frac{1+i}{1-i}$=$\frac{(1+i)^{2}}{(1-i)(1+i)}$=$\frac{2i}{2}$=i,则复数z的虚部等于1.
故选:A.
点评 本题考查了复数相等、复数的运算法则、虚部的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
3.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积是( )
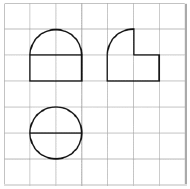

| A. | $\frac{7π}{2}$ | B. | 4π | C. | $\frac{9π}{2}$ | D. | 5π |
7.下列函数中,周期为1的奇函数是( )
| A. | y=cos2πx | B. | y=sinπxcosπx | C. | $y=tan\frac{π}{2}x$ | D. | $y=sin(2πx+\frac{π}{3})$ |
4.已知x∈R,则“|x-3|-|x-1|<2”是“x>3”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |