题目内容
3.已知f(x)是定义在R上的奇函数,且当x>0时,其解析式为f(x)=lgx,那么函数y=f(x)-sinx的零点个数共有( )| A. | 3个 | B. | 4个 | C. | 6个 | D. | 7个 |
分析 本题即求函数f(x)的图象(红线部分)和函数y=sinx的图象(蓝线部分)的交点个数,数形结合可得结论.
解答 解:函数y=f(x)-sinx的零点的个数,
即函数f(x)的图象(红线部分)和函数y=sinx的图象(蓝线部分)的交点个数,
∵f(x)是定义在R上的奇函数,且当x>0时,其解析式为f(x)=lgx,
故两个函数图象如图所示:
显然,函数f(x)的图象(红线部分)和函数y=sinx的图象(蓝线部分)的交点个数为6,
故选:C
点评 本题主要考查函数的两点个数的判断方法,体现了转化以及数形结合的数学思想,属于中档题

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
13.$\int_0^1{3{x^2}dx-\int_0^1{\sqrt{1-{x^2}}dx=}}$( )
| A. | $1-\frac{π}{4}$ | B. | 2 | C. | $1+\frac{π}{4}$ | D. | π-1 |
11.“a≠2”是直线ax+2y=3与直线x+(a-1)y=1相交的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.已知复数$z=\frac{5+3i}{1-i}$,则下列说法正确的是( )
| A. | z的虚部为4i | B. | z的共轭复数为1-4i | ||
| C. | |z|=5 | D. | z在复平面内对应的点在第二象限 |
12.已知A,B分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右顶点,P是C上一点,且直线AP,BP的斜率之积为2,则C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
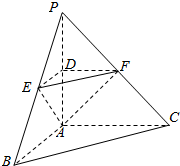 如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥BC,AB⊥AC,PA=1,BC=2.D、E、F分别是棱PA、PB、PC的中点,连接DE、DF、EF.
如图,在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥BC,AB⊥AC,PA=1,BC=2.D、E、F分别是棱PA、PB、PC的中点,连接DE、DF、EF.