题目内容

18．已知复数$z=\frac{5+3i}{1-i}$，则下列说法正确的是（　　）
A．z的虚部为4iB．z的共轭复数为1-4i
C．|z|=5D．z在复平面内对应的点在第二象限

分析 利用复数代数形式的乘除运算化简，求出z，然后逐一核对四个选项得答案．

解答 解：∵$z=\frac{5+3i}{1-i}$=$\frac{（5+3i）（1+i）}{（1-i）（1+i）}=\frac{2+8i}{2}=1+4i$，
∴z的共轭复数为1-4i．
故选：B．

点评 本题考查复数代数形式的乘除运算，考查共轭复数的概念，是基础题．

练习册系列答案
相关题目
8．已知函数f（x）=cos（2x-$\frac{π}{3}$）-cos（2x+$\frac{π}{3}$）+2cos2x-1，x∈R．
（1）求函数f（x）的单调递增区间；
（2）设向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（2，t）（t≠0），$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为α，若f（α）=1，求实数t的值．
9．直线x+a2y+6=0与直线（a-2）x+3ay+2a=0平行，则实数a的值为（　　）
A．3或-1B．0或-1C．-3或-1D．0或3
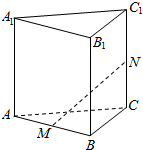6．如图，三棱柱ABC-A1B1C1的棱长都是1，∠BAC=∠BAA1=∠CAA1=60°，点M，N分别是AB，CC1的中点，记$\overrightarrow{AB}$=a，$\overrightarrow{AC}$=b，$\overrightarrow{A{A}_{1}}$=c．
（1）用向量$\overrightarrow{a}$，$\overrightarrow{b}$$\overrightarrow{c}$表示向量$\overrightarrow{MN}$；
（2）求$\overrightarrow{MN}$的模长．
13．设命题p：实数x满足x2-4ax+3a2＜0，其中a＜0；命题q：实数x满足|2x+7|＜5，且?p是?q的必要不充分条件，则实数a的取值范围为[-2，-1]．
3．已知f（x）是定义在R上的奇函数，且当x＞0时，其解析式为f（x）=lgx，那么函数y=f（x）-sinx的零点个数共有（　　）
A．3个B．4个C．6个D．7个
10．化简下列各式
（1）$\frac{\sqrt{3}cos（α+30°）-cos（α+120°）}{cos（a-10°）cos10°+cos（α+80°）cos80°}$．
（2）$\frac{2cos40°+cos10°（1+\sqrt{3}tan10°）}{sin50°cos35°+cos50°cos55°}$．
7．已知点P（x，y）在圆x2+y2-4x-2y+4=0上，则$\frac{y}{x}$的最大值和最小值分别是（　　）
A．1，$\frac{1}{3}$B．$\frac{4}{3}$，0C．$\frac{4}{3}$，-$\frac{4}{3}$D．2，2
8．若f（x）=$\left\{\begin{array}{l}{lg（x-2），x＞0}\\{{x}^{2}-1，x≤0}\end{array}\right.$，则函数y=f（x）的零点是3，-1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网