题目内容
11.“a≠2”是直线ax+2y=3与直线x+(a-1)y=1相交的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 首先,根据两直线平行得到a=2或a=-1,即直线ax+2y=3与直线x+(a-1)y=1相交,则a≠2且a≠-1,从而得到结果.
解答 解:若直线ax+2y=3与直线x+(a-1)y=1平行,
则a(a-1)-2=0,解得a=2或a=-1,
若直线ax+2y=3与直线x+(a-1)y=1相交,则a≠2且a≠-1,
所以“a≠2”是直线ax+2y=3与直线x+(a-1)y=1相交必要不充分条件,
故选:B.
点评 本题重点考查了两直线平行的判断、充条件、必要条件、充要条件等知识,属于基础题.

练习册系列答案
相关题目
1.下列幂函数在定义域内单调递增且为奇函数的是( )
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x2 | C. | y=x3 | D. | y=x-1 |
2.点P(x,y,z)关于坐标平面xOy对称的点的坐标是( )
| A. | (-x,-y,z) | B. | (-x,y,z) | C. | (x,-y,z) | D. | (x,y,-z) |
19.下面4个实数中,最小的数是( )
| A. | sin1 | B. | sin2 | C. | sin3 | D. | sin4 |
16.为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为$\frac{4}{15}$.
(1)请将上面的列联表补充完整
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
(参考公式:${K}^{2}=\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$)
| 常喝 | 不常喝 | 合计 | |
| 肥胖 | 2 | ||
| 不肥胖 | 18 | ||
| 合计 | 30 |
(1)请将上面的列联表补充完整
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1.函数f(x)=sinx-cosx,x∈[0,$\frac{π}{2}$]的最小值为( )
| A. | -2 | B. | -$\sqrt{3}$ | C. | -$\sqrt{2}$ | D. | -1 |
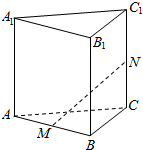 如图,三棱柱ABC-A1B1C1的棱长都是1,∠BAC=∠BAA1=∠CAA1=60°,点M,N分别是AB,CC1的中点,记$\overrightarrow{AB}$=a,$\overrightarrow{AC}$=b,$\overrightarrow{A{A}_{1}}$=c.
如图,三棱柱ABC-A1B1C1的棱长都是1,∠BAC=∠BAA1=∠CAA1=60°,点M,N分别是AB,CC1的中点,记$\overrightarrow{AB}$=a,$\overrightarrow{AC}$=b,$\overrightarrow{A{A}_{1}}$=c.